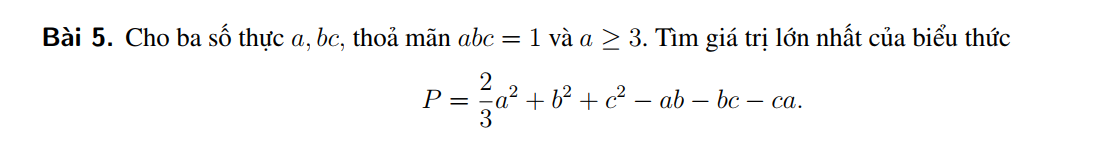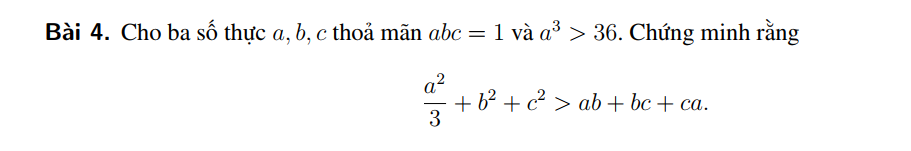Giả sử \(\left(a^4+b^4\right)\left(a^6+b^6\right)\le2\left(a^{10}+b^{10}\right)\)
\(\Leftrightarrow2a^{10}+2b^{10}-a^{10}-a^4b^6-a^6b^4-b^{10}\ge0\\ \Leftrightarrow a^{10}+b^{10}-a^4b^6-a^6b^4\ge0\\ \Leftrightarrow a^4\left(a^6-b^6\right)-b^4\left(a^6-b^6\right)\ge0\\ \Leftrightarrow\left(a^4-b^4\right)\left(a^6-b^6\right)\ge0\\ \Leftrightarrow\left(a-b\right)^2\left(a+b\right)^2\left(a^2+b^2\right)\left(a^2-ab+b^2\right)\left(a^2+ab+b^2\right)\ge0\)
Ta thấy BĐT trên luôn đúng
Suy ra đpcm
Dấu \("="\Leftrightarrow a=b\)
à bạn sửa lại
Dấu \("="\Leftrightarrow a=\pm b\)