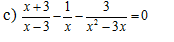a: Xét ΔABC vuông tại A và ΔNIC vuông tại N có
\(\widehat{C}\) chung
Do đó: ΔABC\(\sim\)ΔNIC
Ta có: ΔABC\(\sim\)ΔNIC
nên \(\dfrac{CA}{CN}=\dfrac{CB}{CI}\)
hay \(CA\cdot CI=CB\cdot CN\)
b: Xét ΔABH vuông tại H và ΔCBA vuông tại A có
\(\widehat{B}\) chung
Do đó: ΔABH\(\sim\)ΔCBA
Suy ra: \(\dfrac{BA}{BC}=\dfrac{BH}{BA}\)
hay \(AB^2=BH\cdot BC\)