3a) \(\Delta'=\left(m-1\right)^2-m^2+3m-2=m-1\)
Để pt có 2 nghiệm phân biệt thì \(\Delta>0\Rightarrow m>1\)
b) Áp dụng hệ thức Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=m^2-3m+2\end{matrix}\right.\)
Theo đề: \(x_1^2+x_2^2=3x_1x_2\Rightarrow\left(x_1+x_2\right)^2=5x_1x_2\)
\(\Rightarrow4\left(m-1\right)^2=5m^2-15m+10\Rightarrow m^2-7m+6=0\)
\(\Rightarrow\left(m-1\right)\left(m-6\right)=0\Rightarrow\left[{}\begin{matrix}m=1\\m=6\end{matrix}\right.\) mà \(m>1\Rightarrow m=6\)






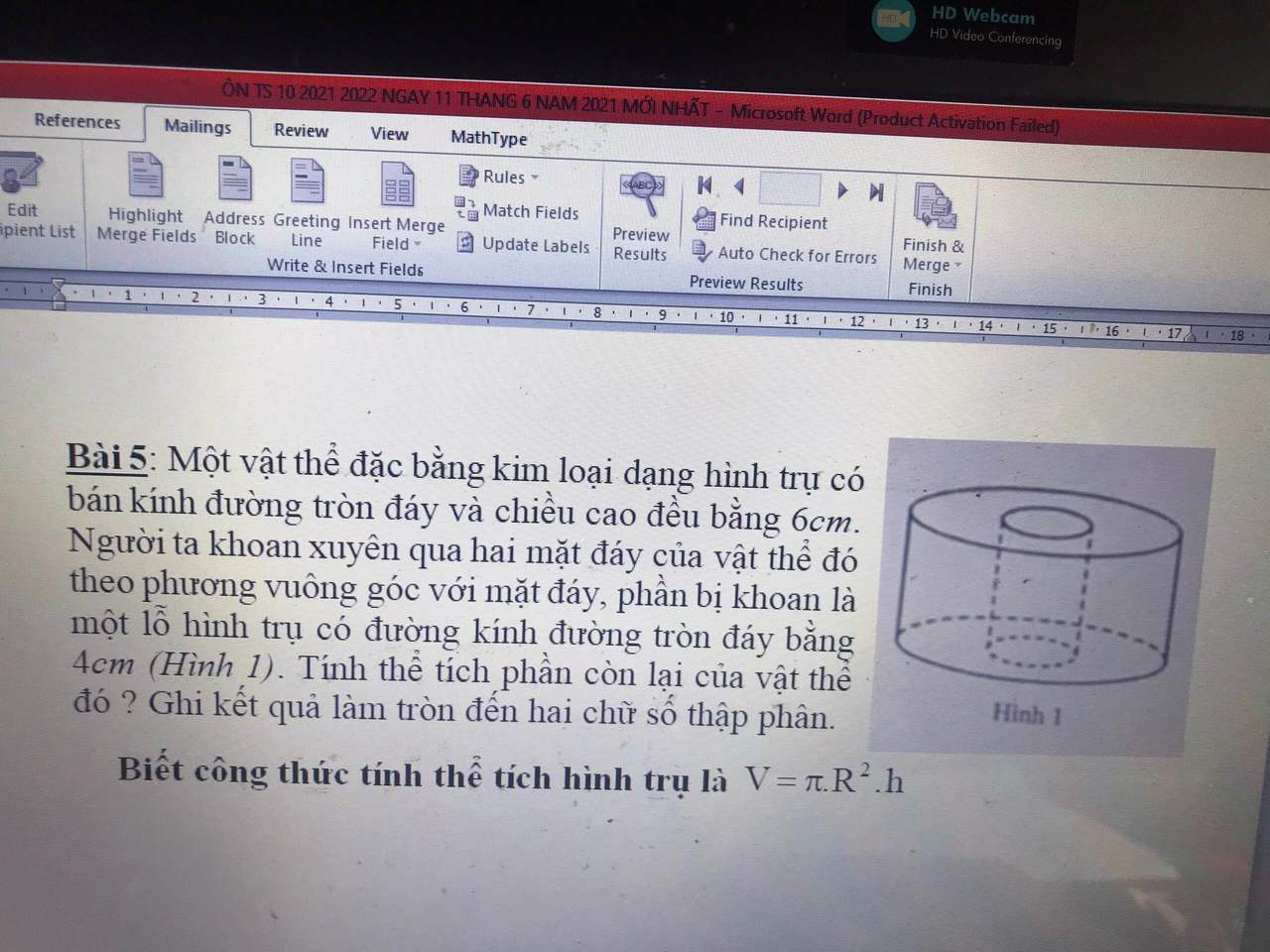

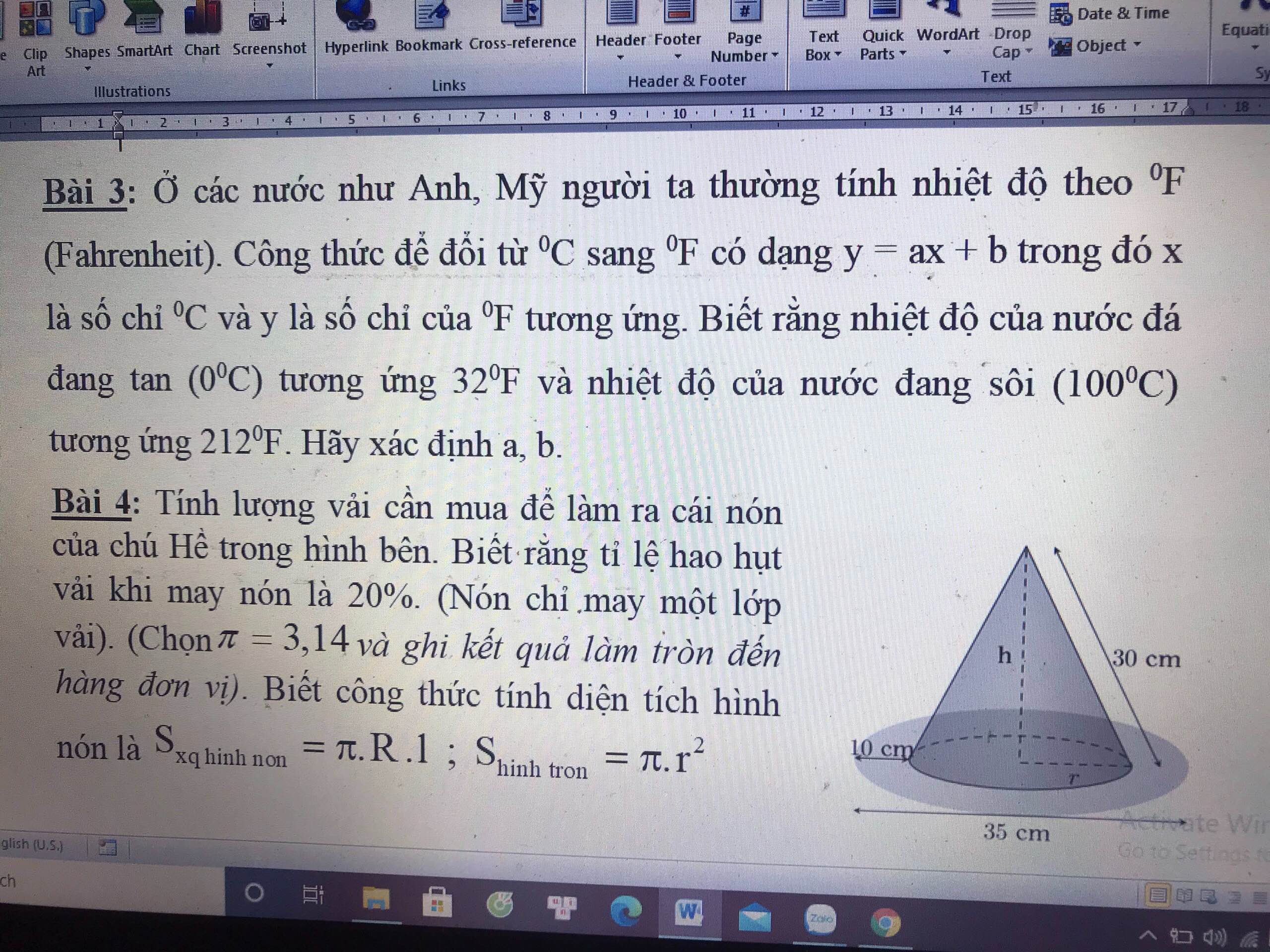
 Mọi người ơi,giúp em bài với ạ em cảm ơn ạ
Mọi người ơi,giúp em bài với ạ em cảm ơn ạ