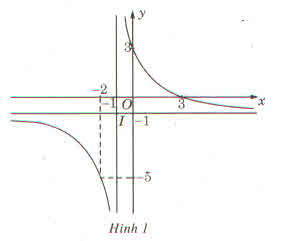
Lời giải:
Trước tiên, ta tìm được đồ thị hàm số $y$ có hai tiệm cận:
\(\bullet\) Tiệm cận đứng \(x=0\) (trục tung \(Oy\))
\(\bullet\) Tiệm cận xiên \(y=3-x\) \((d)\)
Xét hàm \(y=-x+\frac{1}{x}+3\Rightarrow y'=-1-\frac{1}{x^2}\)
Gọi \(a\) là hoành độ tiếp điểm. Khi đó, PT tiếp tuyến là:
\(y=\left ( -1-\frac{1}{a^2} \right )(x-a)-a+\frac{1}{a}+3\)
\(\Leftrightarrow \left ( 1+\frac{1}{a^2} \right )x+y-\frac{2}{a}-3=0\) \((m)\)
Gọi \(A=(d)\cap Oy\) thì \(A(0,3)\)
Gọi \(B=(m)\cap Oy\Rightarrow B(0,\frac{2}{a}+3)\)
Gọi \(C=(d)\cap (m)\). PT hoành độ giao điểm là:
\(-\left (1+\frac{1}{a^2}\right)x+\frac{2}{a}+3=3-x\Leftrightarrow \frac{2}{a}=\frac{x}{a^2}\Leftrightarrow x=2a\)
\(\Rightarrow C(2a,3-2a)\)
Do đó, \(AB=\left | \frac{2}{a} \right |\); \(BC=\sqrt{8a^2+\frac{4}{a^2}+8}\); \(AC=2\sqrt{2}|a|\)
Chu vi tam giác:
\(AB+BC+AC=\left |\frac{2}{a}\right|+2\sqrt{2}|a|+\sqrt{8a^2+\frac{4}{a^2}+8}=2(2+\sqrt{2})\)
\(\Leftrightarrow \left | \frac{1}{a} \right |+\sqrt{2}|a|+\sqrt{2a^2+\frac{1}{a^2}+2}=2+\sqrt{2}\)
Áp dụng BĐT Cô -si:
\(\left | \frac{1}{a} \right |+\sqrt{2}|a|\geq 2\sqrt{\sqrt{2}}>\sqrt{2}\)
\(a^2+\frac{1}{a^2}\geq 2\Rightarrow 2a^2+\frac{1}{a^2}+2\geq 4+a^2\geq 4\)
\(\Rightarrow \left | \frac{1}{a} \right |+\sqrt{2}|a|+\sqrt{2a^2+\frac{1}{a^2}+2}>2+\sqrt{2}\)
Do đó PT vô nghiệm, tức là không tồn tại $a$ nên không tồn tại PTTT.