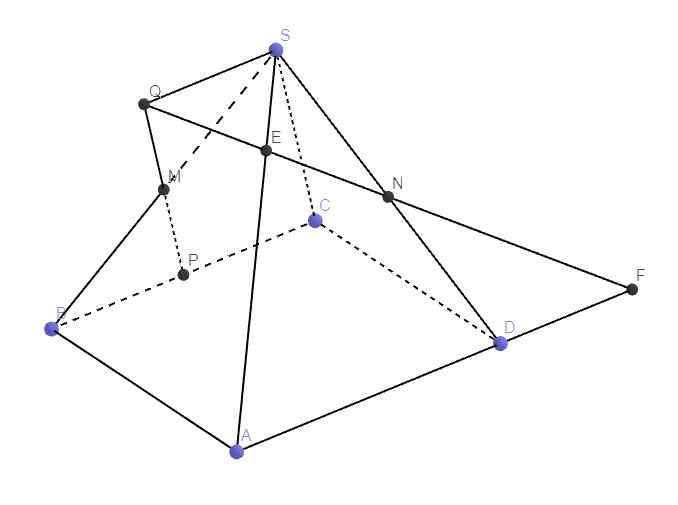
Qua S kẻ đường thẳng d song song BC \(\Rightarrow s=\left(SBC\right)\cap\left(SAD\right)\)
Nối PM kéo dài cắt d tại Q \(\Rightarrow Q\in\left(SAD\right)\)
Trong mp (SAD), nối QN cắt SA tại E và AD tại F
\(\Rightarrow E=SA\cap\left(MNP\right)\)
Do \(SQ||BC\) , theo Talet: \(\dfrac{SQ}{BP}=\dfrac{SM}{BM}=1\Rightarrow SQ=BP=\dfrac{1}{2}BC=\dfrac{1}{2}AD\)
Do \(SQ||AD\Rightarrow\dfrac{SQ}{DF}=\dfrac{SN}{ND}=1\Rightarrow DF=SQ=\dfrac{1}{2}AD\)
\(\Rightarrow AF=AD+DF=\dfrac{3}{2}AD\)
\(\Rightarrow\dfrac{SE}{AE}=\dfrac{SQ}{AF}=\dfrac{\dfrac{1}{2}AD}{\dfrac{3}{2}AD}=\dfrac{1}{3}\Rightarrow SE=\dfrac{1}{3}AE\)
\(\Rightarrow\dfrac{SE}{SA}=\dfrac{1}{4}\)
Đúng 1
Bình luận (0)
