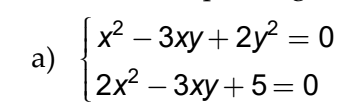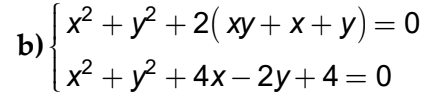\(\left\{{}\begin{matrix}x^2-3xy+2y^2=0\left(1\right)\\2x^2-3xy+5=0\left(2\right)\end{matrix}\right.\)
Ta có:
`(1)<=>x^2 -xy-2xy+2y^2 =0`
`<=>x(x-y)-2y(x-y)=0`
`<=>(x-y)(x-2y)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x=y\\x=2y\end{matrix}\right.\)
Thay `x=y` vào `(2)` ta có:
`2x^2 -3.x.x+5=0`
`<=>2x^2 -3x^2 +5=0`
`<=>-x^2 =-5`
`<=>x^2 =5`
\(\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{5}\Rightarrow y=\sqrt{5}\\x=-\sqrt{5}\Rightarrow y=-\sqrt{5}\end{matrix}\right.\)
Thay `x=2y` vào `(2)` ta có:
`2.(2y)^2 - 3.2y.y+5=0`
`<=>2.4y^2 - 6y^2 +5=0`
`<=>8y^2 -6y^2 = -5`
`<=>2y^2 = -5`(Vô lí)
Vậy `(x,y) in {(sqrt5 , sqrt5);(-sqrt5 , -sqrt5)}`
\(\left\{{}\begin{matrix}x^2+y^2+2\left(xy+x+y\right)=0\left(1\right)\\x^2+y^2+4x-2y+4=0\left(2\right)\end{matrix}\right.\)
Ta có:
`(1) <=> x^2 +2xy + y^2 +2(x+y)=0`
`<=>(x+y)^2 + 2(x+y)=0`
`<=>(x+y)(x+y+2)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x=-y\\x=-y-2\end{matrix}\right.\)
Thay `x=-y` vào `(2)` ta có:
`(-y)^2 + y^2 + 4(-y)-2y+4=0`
`<=>y^2 +y^2 -4y-2y+4=0`
`<=>2y^2 -6y+4=0`
`<=>y^2 -3y+2=0`
\(\Leftrightarrow\left[{}\begin{matrix}y=1\Rightarrow x=-1\\y=2\Rightarrow x=-2\end{matrix}\right.\)
Thay `x=-y-2` vào `(2)` ta có:
`(-y-2)^2 + y^2 + 4(-y-2)-2y+4=0`
`<=>y^2 +4y+4 + y^2 -4y-8-2y+4=0`
`<=>2y^2-2y=0`
`<=>2y(y-1)=0`
\(\Leftrightarrow\left[{}\begin{matrix}y=0\Rightarrow x=-0-2=-2\\y=1\Rightarrow x=-1-2=-3\end{matrix}\right.\)
Vậy `(x,y) in {(-1,1);(-2,2);(-2,0);(-3,1)}`