a, - 1 ≤ cosx ≤ 1 ⇔ - 1 ≤ - cosx ≤ 1
⇔ 4 ≤ 5 - cosx ≤ 6
⇔ 4 ≤ y ≤ 6.
Vậy ymin = 4 khi cosx = 1 ⇔ x = k2π
ymax = 6 khi cosx = - 1 ⇔ x = π + k2π
b, - 1 ≤ sinx ≤ 1 ⇔ - 4 ≤ 4sinx ≤ 4
⇔ - 3 ≤ 4sinx + 1 ≤ 5 ⇔ - 3 ≤ y ≤ 5
ymin = - 3 khi sinx = - 1
ymax = 5 khi sinx = 1
c, sinx - cosx + 7
= \(\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)\) + 7
min = 7 - \(\sqrt{2}\) và max = 7 + \(\sqrt{2}\)
d, Đặt cosx = t ta có hàm số f(t) = 3t2 + t - 2 với t ϵ [- 1 ; 1]
Dùng BBT của hs bậc 2 là được
e, chuyển sin2x = 1 - cos2x
f, \(\sqrt{3}sinx-cosx=2sin\left(x-\dfrac{\pi}{6}\right)\)
g, \(sinx+\sqrt{3}cosx=2sin\left(x+\dfrac{\pi}{3}\right)\)
h, Đặt a = arcsin\(\dfrac{4}{5}\) = arcsin\(\dfrac{3}{5}\)
⇒ 3sinx + 4cosx = 5 sin (x + a) với a = arcsin\(\dfrac{4}{5}\) = arcsin\(\dfrac{3}{5}\)
i, 2sin2x - 1 = - cos2x
k, 7 - 2sin2x . cosx = 7 - (1- cos2x) . cosx
= 7 + cos2x . cosx - cosx
= 7 + \(\dfrac{1}{2}cos3x+\dfrac{1}{2}cosx-cosx\)
= 7 + \(\dfrac{1}{2}cos3x-\dfrac{1}{2}cosx\)
Ta có - 1 ≤ cos3x ≤ 1; -1 ≤ - cosx ≤ 1
nên cos3x - cosx ∈ [- 2 ; 2]
Từ đó suy ra min max. Dấu bằng có xảy ra






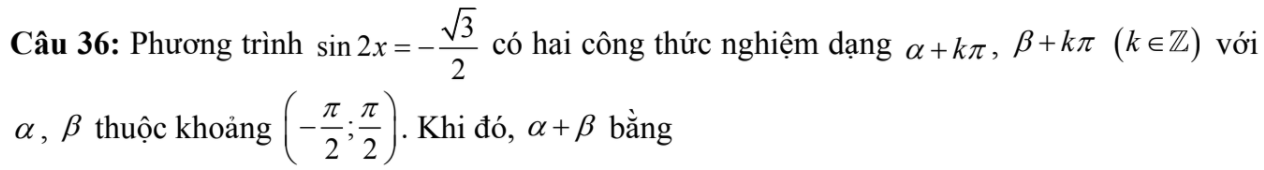 giúp mk với ạ
giúp mk với ạ