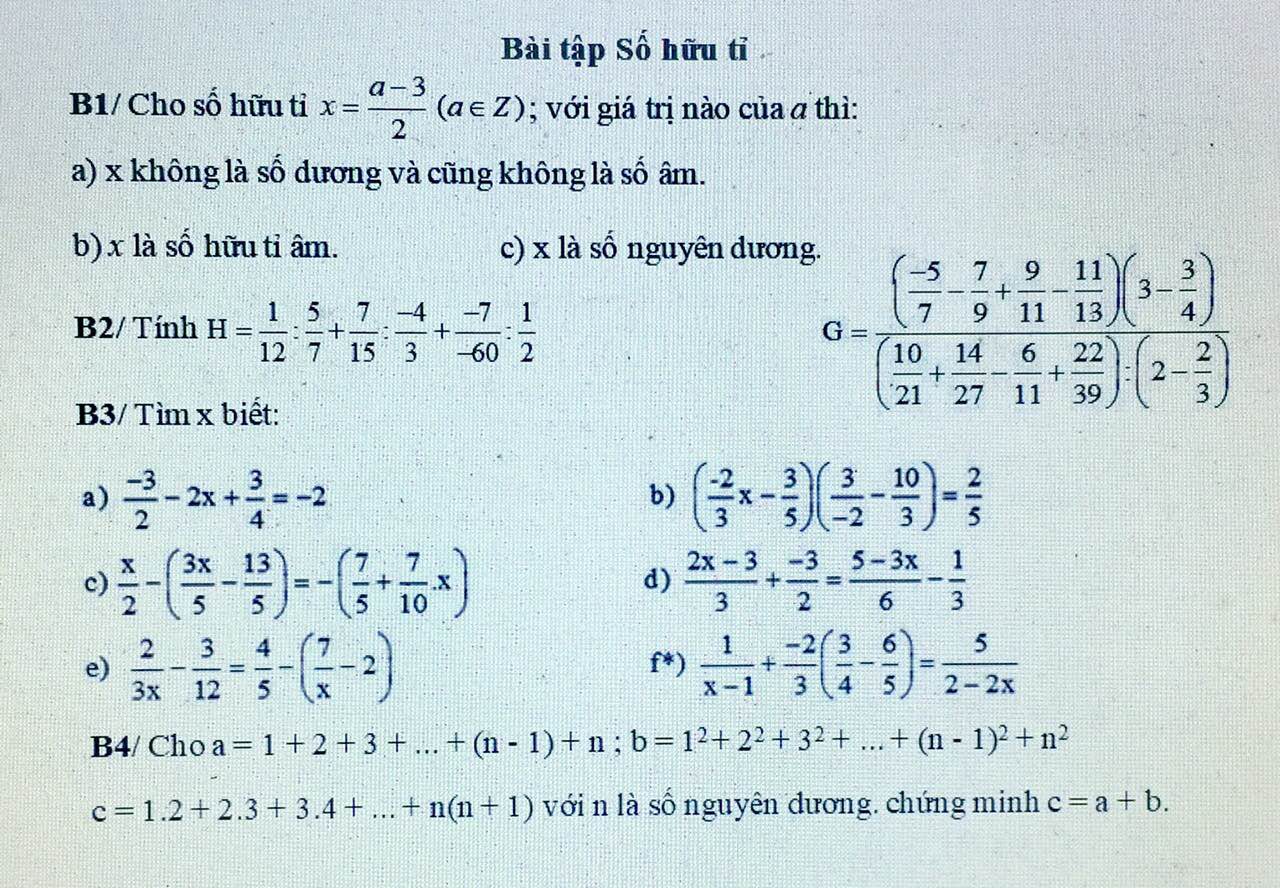Bài 4:
Số số hạng của dãy A là:
n-1+1=n(số)
Tổng của dãy A là:
\(a=\dfrac{\left(n+1\right)\cdot n}{2}\)
Ta có: \(b=1^2+2^2+3^2+...+\left(n-1\right)^2+n^2\)
\(=1+2\left(1+1\right)+3\left(2+1\right)+...+n\left(n-1+1\right)\)
\(=\dfrac{n\left(n+1\right)}{2}+\dfrac{n\left(n+1\right)\left(n-1\right)}{3}\)
\(=\dfrac{3n\left(n+1\right)}{6}+\dfrac{2n\left(n+1\right)\left(n-1\right)}{6}\)
\(=\dfrac{n\left(n+1\right)\left(2n+1\right)}{6}\)
Ta có: \(c=1\cdot2+2\cdot3+3\cdot4+...+n\left(n+1\right)\)
\(\Leftrightarrow3c=1\cdot2\cdot3+2\cdot3\cdot4+3\cdot4\cdot3+...+3n\left(n+1\right)\)
\(\Leftrightarrow3c=n\left(n+1\right)\left(n+2\right)\)
\(\Leftrightarrow c=\dfrac{n\left(n+1\right)\left(n+2\right)}{3}\)
Ta có: \(a+b=\dfrac{\left(n+1\right)n}{2}+\dfrac{n\left(n+1\right)\left(2n+1\right)}{6}\)
\(=\dfrac{3n\left(n+1\right)+n\left(n+1\right)\left(2n+1\right)}{6}\)
\(=\dfrac{n\left(n+1\right)\left(3+2n+1\right)}{6}\)
\(=\dfrac{n\left(n+1\right)\left(2n+4\right)}{6}\)
\(=\dfrac{n\left(n+1\right)\left(n+2\right)}{3}\)
=c(đpcm)