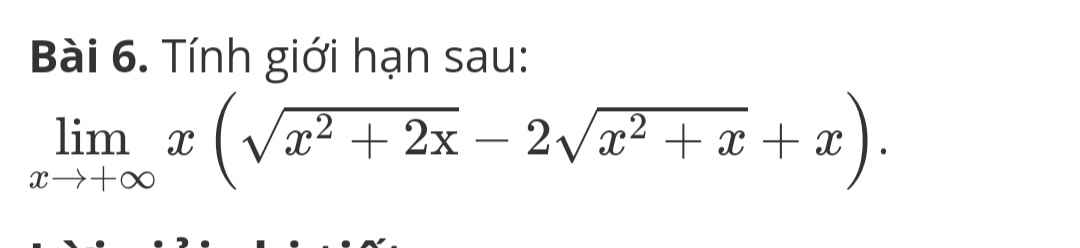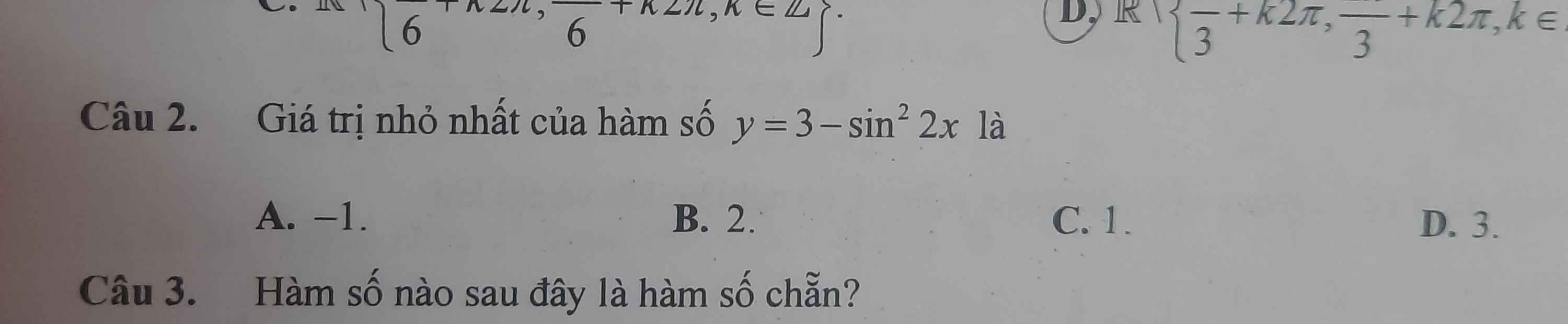Các công thức lượng giác cơ bản liên quan đến góc của lớp 10:
\(sin\left(3\pi-x\right)=sin\left(2\pi+\pi-x\right)=sin\left(\pi-x\right)=sinx\)
\(sin\left(\dfrac{\pi}{2}+x\right)=cosx\Rightarrow sin\left(\dfrac{5\pi}{2}+x\right)=sin\left(2\pi+\dfrac{\pi}{2}+x\right)=sin\left(\dfrac{\pi}{2}+x\right)=cosx\)
\(cos\left(\dfrac{\pi}{2}+x\right)=-sinx\)
\(sin\left(\dfrac{3\pi}{2}+x\right)=sin\left(2\pi-\dfrac{\pi}{2}+x\right)=sin\left(-\dfrac{\pi}{2}+x\right)=-cosx\)
Nên pt tương đương:
\(3sin^2x-2sinx.cosx-5cos^2x=0\)
Với \(cosx=0\) không là nghiệm
Với \(cosx\ne0\) chia 2 vế cho \(cos^2x\)
\(\Rightarrow3tan^2x-2tanx-5=0\)
\(\Rightarrow\left[{}\begin{matrix}tanx=-1\\tanx=\dfrac{5}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=arctan\left(\dfrac{5}{3}\right)+k\pi\end{matrix}\right.\)