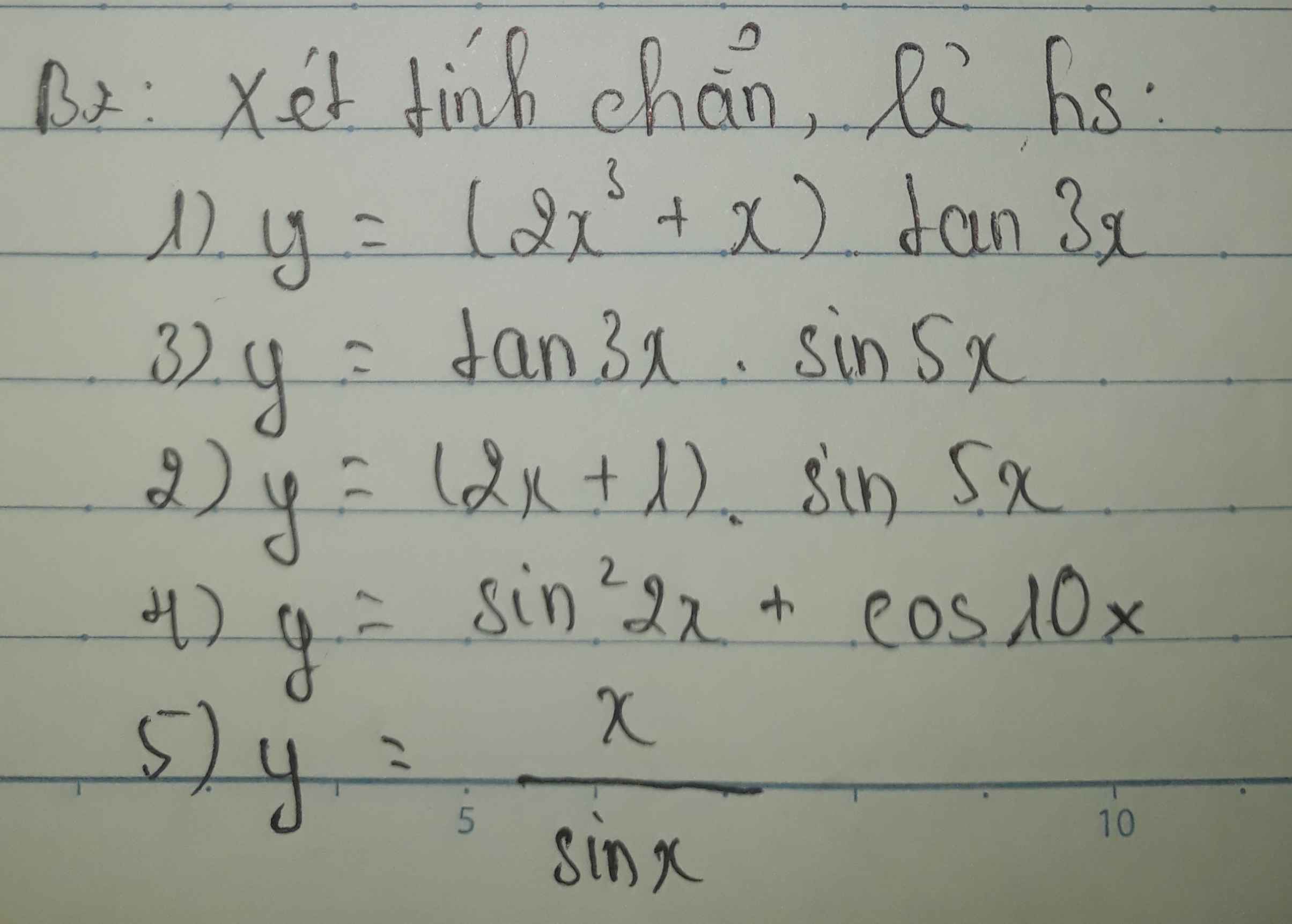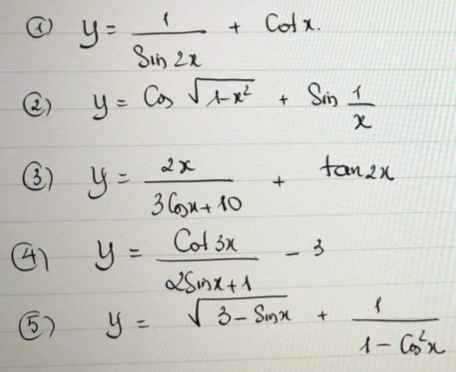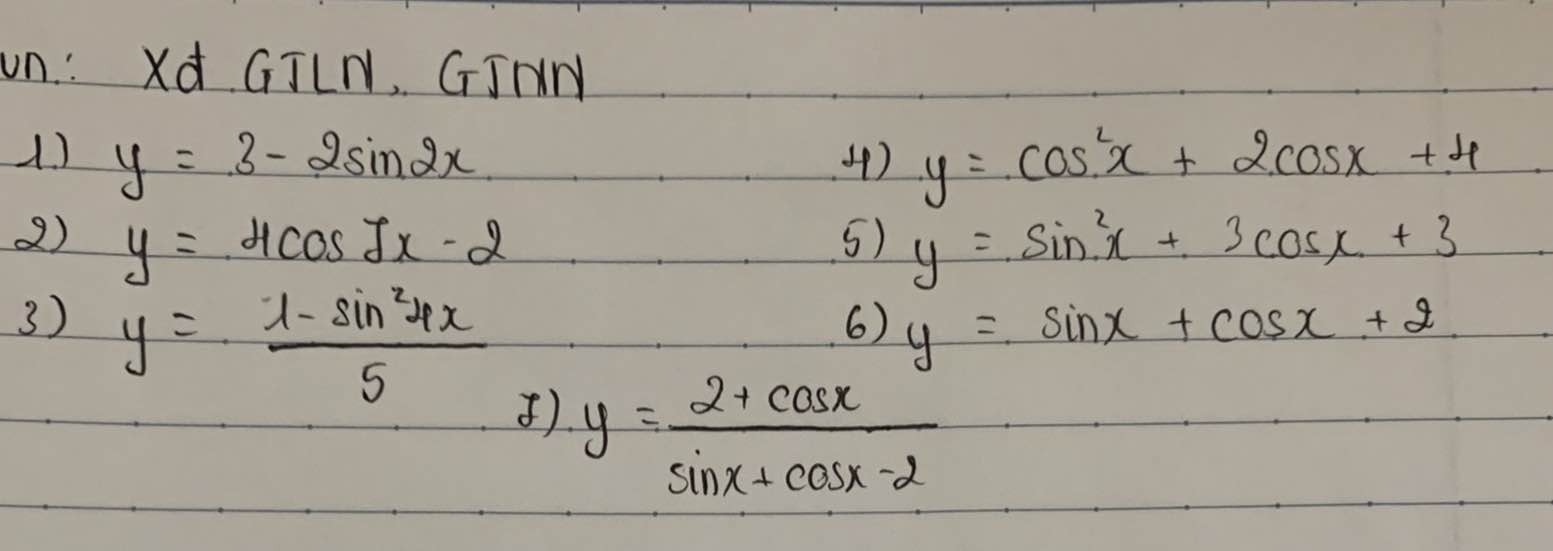3.
\(y=\dfrac{1-sin^24x}{5}=\dfrac{cos^24x}{5}\)
\(cos4x\in\left[-1;1\right]\Rightarrow cos^24x\in\left[0;1\right]\Rightarrow y\in\left[0;\dfrac{1}{5}\right]\Rightarrow\left\{{}\begin{matrix}y_{min}=0\\y_{max}=\dfrac{1}{5}\end{matrix}\right.\)
6.
\(y=sinx+cosx+2=\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)+2\)
\(sin\left(x+\dfrac{\pi}{4}\right)\in\left[-1;1\right]\Rightarrow y=\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)+2\in\left[-\sqrt{2}+2;\sqrt{2}+2\right]\)
\(\Rightarrow y_{min}=-\sqrt{2}+2\)
\(y_{max}=\sqrt{2}+2\)
1.
\(sin2x\in\left[-1;1\right]\Rightarrow y=3-2sin2x\in\left[1;5\right]\)
\(\Rightarrow\left\{{}\begin{matrix}y_{min}=1\\y_{max}=5\end{matrix}\right.\)
2.
\(cos7x\in\left[-1;1\right]\Rightarrow y=4cos7x-2\in\left[-6;2\right]\Rightarrow\left\{{}\begin{matrix}y_{min}=-6\\y_{max}=2\end{matrix}\right.\)
4.
Đặt \(cosx=t\left(t\in\left[-1;1\right]\right)\)
\(\Rightarrow y=f\left(t\right)=t^2+2t+4\)
\(\Rightarrow y_{min}=minf\left(t\right)=f\left(-1\right)=3\)
\(y_{max}=maxf\left(t\right)=f\left(1\right)=7\)
5.
\(y=sin^2x+3cosx+3=-cos^2x+3cosx+4\)
Đặt \(cosx=t\left(t\in\left[-1;1\right]\right)\).
\(\Rightarrow y=f\left(t\right)=-t^2+3t+4\)
\(\Rightarrow y_{min}=minf\left(t\right)=0\)
\(y_{max}=maxf\left(t\right)=6\)