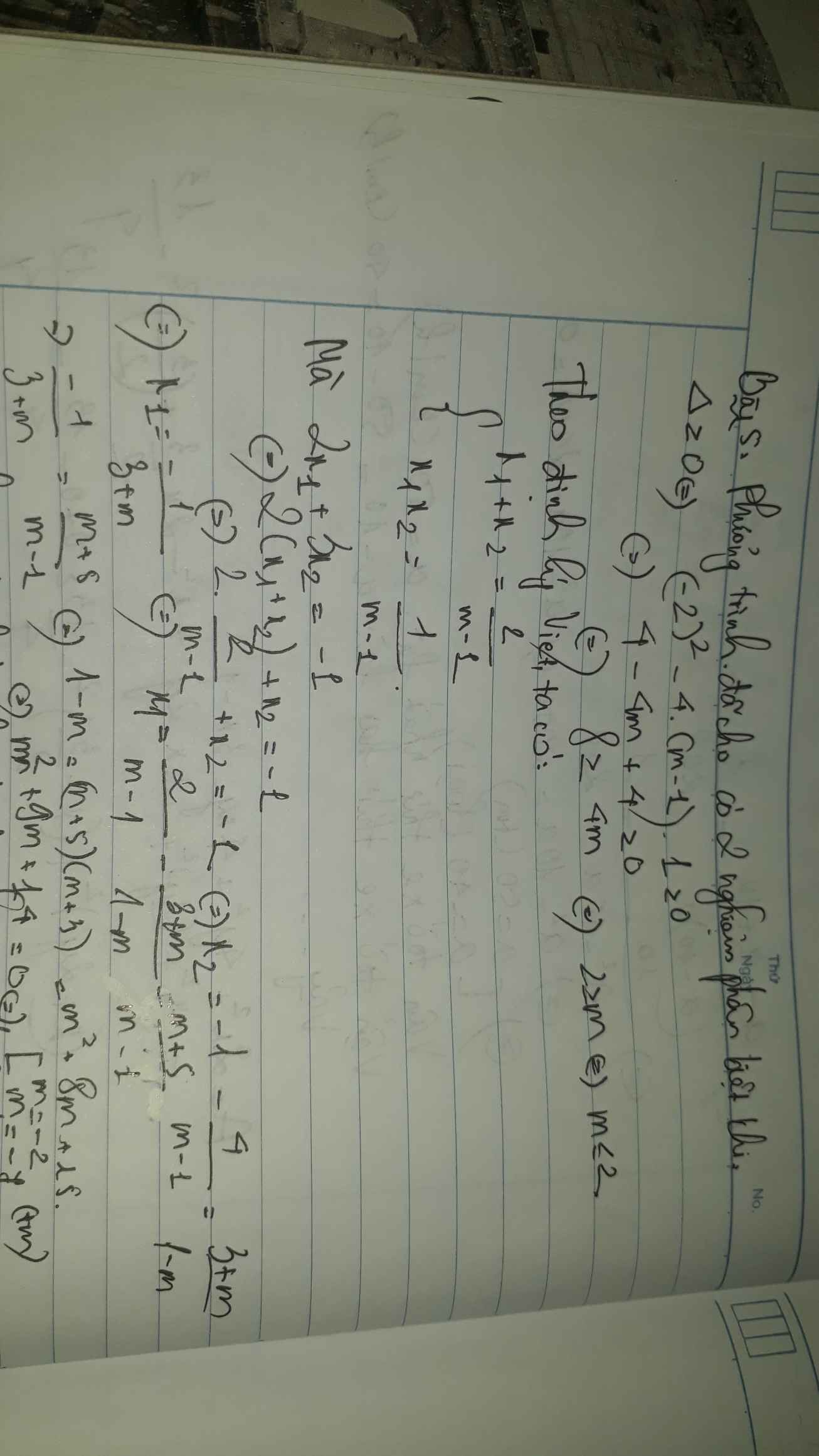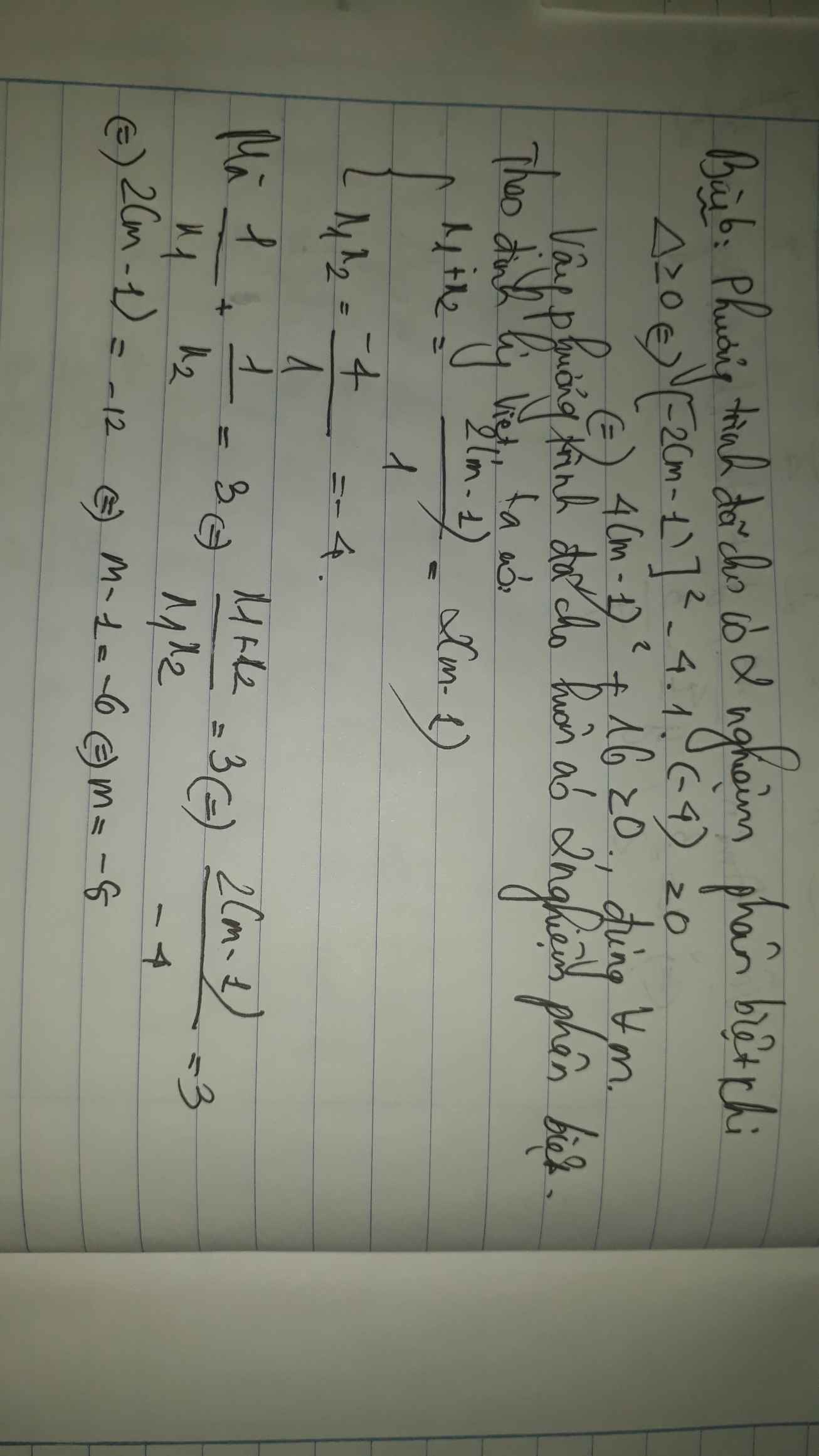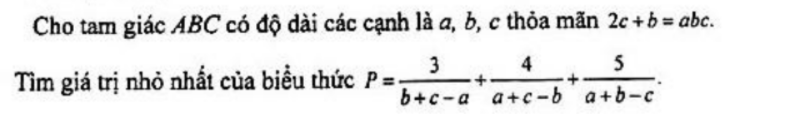[Toán+Hóa C56-17.8.21 (Yến Nguyễn)]





Bài 1:
a)Ta có: Δ= m2-4.1.(2m-4)=m2-8m+16=(m-4)2≥0
⇒ phương trình luôn có nghiệm với mọi giá trị của m
b)Theo hệ thức Viet ta có:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-m}{1}=-m\\x_1x_2=\dfrac{2m-4}{1}=2m-4\end{matrix}\right.\)
Ta có: x12+x22 = 4
⇔ (x1+x2)2-2x1x2=4
⇒ m2-2.(2m-4)=4
⇔ m2-4m+8=4
⇔ m2-4m+4=0
⇔ (m-2)2=0 ⇔ m=2
Bài 2:
a)x2-2x+m-1=0 (1)
Thay m=-2 vào phương trình ta có:
(1)⇔x2-2x-3=0
\(\Leftrightarrow\left(x-3\right)\left(x+1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-1\end{matrix}\right.\)
b)Theo hệ thức Viet ta có:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(1\right)\\x_1x_2=m-1\left(2\right)\end{matrix}\right.\)
Theo bài ra,ta có:x1=2x2
Kết hợp với (1) ta có hpt:
\(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=2\\x_1-2x_2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{4}{3}\\x_2=\dfrac{2}{3}\end{matrix}\right.\)
\(\Rightarrow\left(2\right)\Leftrightarrow\dfrac{4}{3}\cdot\dfrac{2}{3}=m-1\Leftrightarrow m=\dfrac{17}{9}\)
Bài 6:
\(\Delta=\left(-2\right)^2-4\cdot\left(m-1\right)\cdot1\)
\(=4-4m+4\)
\(=-4m+8\)
Để phương trình có hai nghiệm phân biệt thì \(\Delta>0\)
\(\Leftrightarrow-4m>-8\)
hay m<2
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2}{m-1}\\x_1x_2=\dfrac{1}{m-1}\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2}{m-1}\\2x_1+3x_2=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x_1+2x_2=\dfrac{4}{m-1}\\2x_1+3x_2=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-x_2=\dfrac{m+3}{m-1}\\x_1+x_2=\dfrac{2}{m-1}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{-m-3}{m-1}\\x_1=\dfrac{2}{m-1}-\dfrac{-m-3}{m-1}=\dfrac{2+m+3}{m-1}=\dfrac{m+5}{m-1}\end{matrix}\right.\)
Ta có: \(x_1x_2=\dfrac{1}{m-1}\)
\(\Leftrightarrow\dfrac{m+5}{m-1}\cdot\dfrac{-m-3}{m-1}=\dfrac{1}{m-1}\)
\(\Leftrightarrow\dfrac{-\left(m+5\right)\left(m+3\right)}{\left(m-1\right)^2}=\dfrac{m-1}{\left(m-1\right)^2}\)
Suy ra: \(-m^2-8m-15-m+1=0\)
\(\Leftrightarrow-m^2-9m-14=0\)
\(\Leftrightarrow m^2+9m+14=0\)
\(\Leftrightarrow\left(m+2\right)\left(m+7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=-2\left(nhận\right)\\m=-7\left(nhận\right)\end{matrix}\right.\)
Lúc trưa đang làm thì đột nhiên cúp điện.......
Toán C56 bài 6