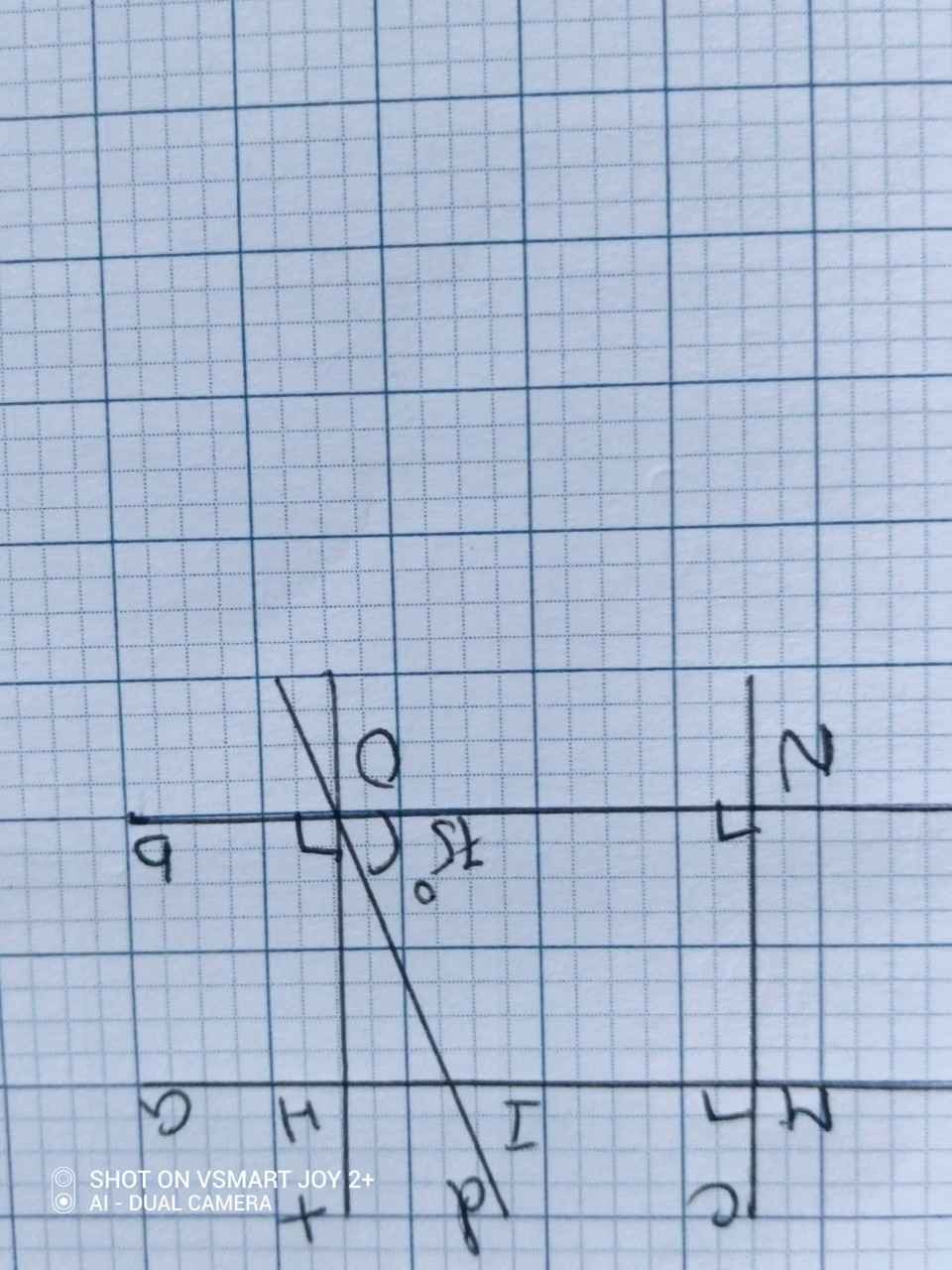ta có: \(\left\{{}\begin{matrix}a\perp MN\\a\perp PQ\end{matrix}\right.\)
⇒ MN // PQ
⇒ \(\widehat{PBA}=\widehat{MAC}\) (2 góc đồng vị)
vì BA là tia phân giác của \(\widehat{PBD}\) \(\Rightarrow\widehat{PBA}=\frac{1}{2}\widehat{PBD}=\frac{1}{2}.90^o=45^o\)
\(\Rightarrow\widehat{MAC}=45^o\)
\(\Rightarrow\widehat{DAB}=\widehat{MAC}=45^o\) (2 góc đối đỉnh)
ta có: \(\widehat{MAC}+\widehat{CAD}=180^o\) (2 góc kề bù)
hay \(45^o+\widehat{CAD}=180^o\)
\(\Rightarrow\widehat{CAD}=180^o-45^o=135^o\)
\(\Rightarrow\widehat{MAB}=\widehat{CAD}=135^o\) (2 góc đối đỉnh)
vậy \(\widehat{DAB}=\widehat{MAC}=45^o,\widehat{MAB}=\widehat{CAD}=135^o\)