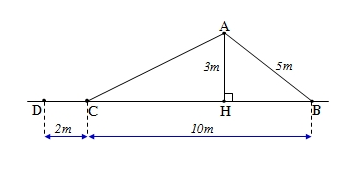
Xét tam giác vuông AHB (^AHB = 90°) ta có:
AB2 = AH2 + HB2 (vì bình phương cạnh huyền bằng tổng bình phương 2 cạnh góc vuông).
hay 52 = 32 + HB2
=> HB2 = 52 - 32 = 25 - 9 = 16.
HB = \(\sqrt{16}\) = 4.
Vậy HB = 4m.
Độ dài cạnh CH là:
CH = BC - HB
hay CH = 10 - 4 = 6 (m)
Vậy cạnh CH = 6m.
Xét tam giác vuông AHC (^AHC = 90°) ta có:
AC2 = AH2 + CH2
hay AC2 = 32 + 62 = 9 + 36 = 45.
AC = \(\sqrt{45}\approx7.\)
Vậy AC \(\approx7m\).
Độ dài ACD là:
ACD = AC + CD
hay ACD = 7 + 2 = 9 (m).
Vậy ACD = 9m.
2 lần BA là:
5.2 = 10 (m)
Vậy 2 lần BA = 10m.
Mà ACD < BA (9 < 10) nên đường trượt ACD ko gấp hơn hai lần đường lên BA.
Vậy bạn Mai nói sai, bạn Vân nói đúng.
Tam giác AHB vuông tại H nên theo định lí Pi-ta-go ta có:
HB2 = AB2 - AH2 = 52 - 32 = 25 - 9 = 16
Suy ra HB = 4 (m)
Và HC = BC - HB = 10 -4 = 6 (m)
Tam giác AHC vuông tại H nên AC2 = AH2 + HC2 = 32 + 62 = 9 + 36 = 45
Suy ra AC = √45
Độ dài đường trượt ACD bằng:
6,7 + 2 = 8,7 (m)
Và hai lần đường lên BA bằng 5.2 = 10 (m)
Đo độ dài đường trượt ACD chưa bằng hai lần đường lên BA
Vậy bạn Mai nói sai, bạn Vân nói đúng
+ ΔAHB vuông tại H
Theo định lí Py–ta- go ta có
HB2 = AB2 – AH2 = 52 – 32 =25 - 9 =16
Suy ra HB = 4 (cm)
Suy ra HC = BC – HB = 10 - 4 = 6(cm)
+ ΔAHC vuông tại H
Theo định lí Py-ta-go ta có
AC2 = AH2 + HC2 = 32 + 62 = 9 + 36 = 45.
Suy ra AC = √45 ≈ 6,7(m)
Độ dài đường trượt ACD bằng: 6,7 + 2= 8,7 (m)
Và hai lần đường lên BA bằng 5.2 =10 (m)
Đo độ dài đường trượt ACD chưa bằng hai lần đườg lên BA
Vậy bạn Mai nói sai, bạn Vân nói đúng.