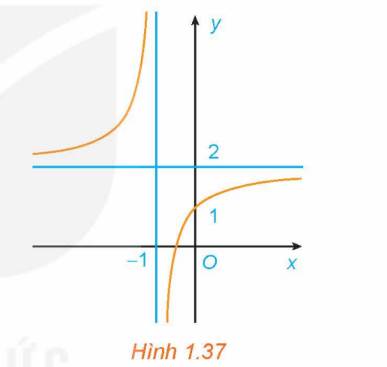
Đồ thị hàm số trong hình 1.37 có tiệm cận ngang là \(y = 2\).
Xét hàm số: \(y = \frac{{2x + 1}}{{x + 1}}\) có: \(\mathop {\lim }\limits_{x \to + \infty } \frac{{2x + 1}}{{x + 1}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2 + \frac{1}{x}}}{{1 + \frac{1}{x}}} = 2\) nên đồ thị hàm số \(y = \frac{{2x + 1}}{{x + 1}}\) có tiệm cận ngang là \(y = 2\).
Đường thẳng \(y = 2\) không là tiệm cận ngang của các đồ thị hàm số \(y = \frac{{x - 1}}{{x + 1}}\); \(y = \frac{{x + 3}}{{1 - x}}\); \(y = \frac{{x + 2}}{{x + 1}}\).
Chọn B.
Đúng 0
Bình luận (0)