
Từ đồ thị ta dễ dàng thấy được có 4 giá trị trên đoạn \(\left[-2\pi;2\pi\right]\) thỏa mãn điều kiện \(tan\left(x\right)=2\)

Từ đồ thị ta dễ dàng thấy được có 4 giá trị trên đoạn \(\left[-2\pi;2\pi\right]\) thỏa mãn điều kiện \(tan\left(x\right)=2\)
Dựa vào đồ thị của hàm số \(y = sinx\), xác định các giá trị \(x \in [ - \pi ;\pi ]\;\)thoả mãn \(sinx = \frac{1}{2}\)
Tìm tập xác định của các hàm số sau:
\(\begin{array}{l}a)\;y = \frac{1}{{cosx}}\\b)\;y = tan(x + \frac{\pi }{4})\\c)\;y = \frac{1}{{2 - si{n^2}x}}\end{array}\)
Li độ s (cm) của một con lắc đồng hộ theo thời gian t (giây) được cho bởi hàm số \(s = 2\cos \pi t\). Dựa vào đồ thị của hàm số côsin, hãy xác định ở các thời điểm t nào trong 1 giây đầu thì li độ s nằm trong đoạn \(\left[ { - 1;1} \right]\,\,(cm)\).

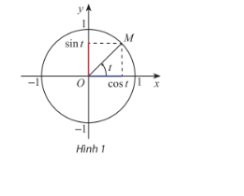
Cho số thực t và M là điểm biểu diễn của góc lượng giác có số đo t rad trên đường tròn lượng giác. Sử dụng định nghĩa của các giá trị lượng giác, hãy giải thích vì sao xác định duy nhất:
a) Giá trị sint và cost
b) Giá trị tant (nếu \(t \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\)) và \(\cot t\)(nếu \(t \ne k\pi ,k \in \mathbb{Z}\)).
Trong Hình 13, một chiếc máy bay A bay ở độ cao 500m theo một đường thẳng đi ngang qua phía trên trạm quan sát T ở mặt đất. Hình chiếu vuông góc của A lên mặt đất là H, \(\alpha \) là góc lượng giác \((Tx,{\rm{ }}TA)\) \((0 < \alpha < \pi ).\)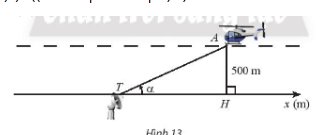
a) Biểu diễn toạ độ \({x_H}\) của điểm H trên trục \({T_x}\) theo \(\alpha \).
b) Dựa vào đồ thị hàm số côtang, hãy cho biết với \(\frac{\pi }{6} < \alpha < \frac{{2\pi }}{3}\) thì \({x_H}\) nằm trong khoảng nào. Làm tròn kết quả đến hàng phần mười.
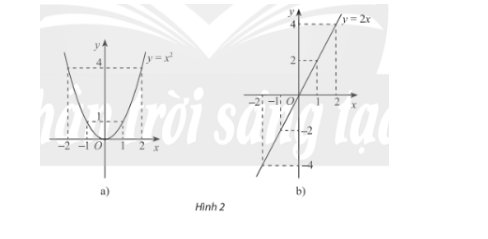
Xét hai hàm số \(y = {x^2},y = 2x\) và đồ thị của chúng trong Hình 2. Đối với mỗi trường hợp, nêu mối liên hệ của giá trị hàm số tại 1 và -1, 2 và -2. Nhận xét về tính đối xứng của mỗi đồ thị hàm số.
Hoàn thành bảng giá trị sau đây:

Hoàn thành bảng giá trị sau đây:

Hoàn thành bảng giá trị sau đây:
