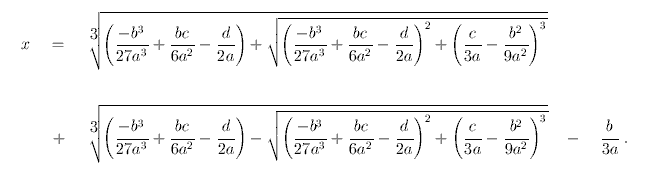Thôi giải luôn cái phương trình bậc 3 vậy.
\(x^3-8x^2+25x-2037=0\left(1\right)\)
Ta có:
\(\left\{{}\begin{matrix}\Delta=b^2-3ac=-11< 0\\k=\dfrac{9abc-2b^3-27a^2d}{2\sqrt{\left|\Delta\right|^3}}\approx746,83\end{matrix}\right.\)
Vì \(\Delta< 0\) nên pt có nghiệm duy nhất là:
\(x=\dfrac{\sqrt{\left|\Delta\right|}}{3a}.\left(\sqrt[3]{k+\sqrt{k^2+1}}+\sqrt[3]{k-\sqrt{k^2+1}}\right)-\dfrac{b}{3a}\approx15,2\)
Vì sai số nên đáp án chỉ là xấp xỉ thôi. Đúng phải là: 15,18632....
Làm biếng nghĩ lắm. Có công thức thì áp vô luôn cho khỏe.
\(\left(x-3\right)^3+\left(x-2\right)^2+\left|x-1\right|+x=2013\)
Xét 2 trường hợp :
TH1: \(\left|x-1\right|\ge1\) với \(x\ge1\)
Ta có:
\(\left(x-3\right)^3+\left(x-2\right)^2+x+1+x=2013\) (1)
\(\Leftrightarrow x^3-9x^2+27x-27+x^2-4x+4+x-1+x=2013\)\(\Leftrightarrow x^3-8x^2+25x-2037=0\)
Đặt \(t=x-\dfrac{8}{3}\) ta được:
\(\left(1\right)\Leftrightarrow\left(t+\dfrac{8}{3}\right)^3-8\left(t+\dfrac{8}{3}\right)^2+25\left(t+\dfrac{8}{3}\right)-2037=0\)\(\Leftrightarrow t^3+\dfrac{11}{3}t-\dfrac{54223}{27}=0\) (2)
Đặt \(y=\dfrac{t}{2.\dfrac{\sqrt{11}}{3}}=\dfrac{t}{\dfrac{2\sqrt{11}}{3}}\Rightarrow t=\dfrac{2\sqrt{11}}{3}y\)
Khi đó: \(\left(2\right)\Leftrightarrow\left(\dfrac{2\sqrt{11}}{3}y\right)^3+\dfrac{11}{3}.\dfrac{2\sqrt{11}}{3}y-\dfrac{54223}{27}=0\)\(\Leftrightarrow\dfrac{22\sqrt{11}}{27}\left(4y^3+3y-743,129529\right)=0\)
\(\Leftrightarrow4y^3+3y-743,129529=0\) (3)
Giả sử \(y_0\) là nghiệm của phương trình , khi đó:
- Với \(y>y_0\) thì :
\(\left\{{}\begin{matrix}4y^3>4y_0^3\\3y>3y_0\end{matrix}\right.\Rightarrow4y^3+3y>4y_0^3+3y_0=743,129529\)\(\Rightarrow\) pt vô nghiệm
- Với \(y< y_0\) thì
\(\left\{{}\begin{matrix}4y^3< 4y^3_0\\3y< 3y_0\end{matrix}\right.\Rightarrow4y^3+3y< 4y_0^3+3y_0=743,129529\)\(\Rightarrow\) pt vô nghiệm
Vậy (3) nếu có nghiệm \(y_0\) thì nghiệm đó là duy nhất.
Đặt : \(a=\sqrt[3]{743,129529+\sqrt{743,129529^2+1}}\)
\(\alpha=\dfrac{1}{2}\left(a-\dfrac{1}{a}\right)\) ta được:
\(4\alpha^3+3\alpha=743,129529\) \(\Rightarrow\alpha=y\)là nghiệm của pt
\(\Rightarrow y=\dfrac{1}{2}\cdot\left(\sqrt[3]{743,129529+\sqrt{743,129529^2+1}}+\dfrac{1}{\sqrt[3]{743,129529+\sqrt{743,129529^2+1}}}\right)\)\(=5,662228051\)
\(\Rightarrow\) \(t=\dfrac{2\sqrt{11}}{3}.5662228051=12,51965728\)
\(\Rightarrow x=12,51965728+\dfrac{8}{3}=15,18632395\)
TH2: \(\left|x-1\right|< 1\) với x < 1
Ta có:
\(\left(x-3\right)^3+\left(x-2\right)^2-x+1+x=2013\) (1)
\(\Leftrightarrow x^3-9x^2+27x-27+x^2-4x+4-x+1+x-2013=0\)\(\Leftrightarrow x^3-8x^2+23x-2035=0\)
Đặt \(t=x-\dfrac{8}{3}\Rightarrow x=t+\dfrac{8}{3}\) , ta đươc:
\(\left(1\right)\Leftrightarrow\left(t+\dfrac{8}{3}\right)^3-8\left(t+\dfrac{8}{3}\right)^2+23\left(t+\dfrac{8}{3}\right)-2035=0\)\(\Leftrightarrow t^3+\dfrac{5}{3}t-\dfrac{54313}{27}=0\) (2)
Đặt \(y=\dfrac{t}{2.\sqrt{\dfrac{5}{9}}}=\dfrac{t}{\dfrac{2\sqrt{5}}{3}}\Rightarrow t=\dfrac{2\sqrt{5}}{3}y\)
Khi đó :
\(\left(2\right)\Leftrightarrow\left(\dfrac{2\sqrt{5}}{3}y\right)^3+\dfrac{5}{3}.\dfrac{2\sqrt{5}}{3}-\dfrac{54313}{27}=0\)
\(\Leftrightarrow4y^3+3y=2428,951201\) (3)
Chứng minh (3) có 1 nghiệm duy nhất ( cmtren)
Đặt \(a=\sqrt[3]{2428,951201+\sqrt{2428,951201^2+1}}\)
\(\alpha=\dfrac{1}{2}\left(a-\dfrac{1}{a}\right)\) , ta được:
\(4\alpha^3-3\alpha=2428,951201\Leftrightarrow y=\alpha\) là nghiệm của pt
Khi đó:
\(y=\dfrac{1}{2}\left(\sqrt[3]{2428,951201+\sqrt{2428,951201^2+1}}+\dfrac{1}{\sqrt[3]{2428,951201+\sqrt{2428,951201^2+1}}}\right)\)=\(8,438583197\)
\(\Rightarrow t=\dfrac{2\sqrt{5}}{3}.8,438583197=12,57949826\)
\(\Rightarrow x=12,57949826+\dfrac{8}{3}=15,24616493\)
Phần thưởng đã được trao cho anh Hùng nhé!
-xét x\(\ge\)1;x<1
-nhân hết ra rồi thay a,b,c vào đây là tìm được nghiệm :)
Xét \(x< 1\)
\(\Rightarrow\left(x-3\right)^3+\left(x-2\right)^2+1-x+x=2013\)
\(\Leftrightarrow\left(x-3\right)^3+\left(x-2\right)^2=2012\)
Ta thấy \(\left\{{}\begin{matrix}VT< 0\\VP>0\end{matrix}\right.\) nên phương trình vô nghiệm
Xét \(x\ge1\)
\(\Rightarrow\left(x-3\right)^3+\left(x-2\right)^2+x-1+x=2013\)
\(\Leftrightarrow x^3-8x^2+25x-2037=0\)
Tới đây thì
(1) Bấm máy tính ra nghiệm luôn.
(2) Dùng công thức Cardano làm tiếp.
Gợi ý: có thể giá trị x tồn tại và x không tồn tại
Gợi ý: có thể x tồn tại hoặc x không tồn tại
Đáp án:
Giải:
\(x-3,x-2,x-1,x\) là 4 số nguyên liên tiếp nên sẽ có 2 số lẻ và hai số chẵn
\(\Rightarrow\left(x-3\right)^3,\left(x-2\right)^2,\left|x-1\right|+\left|x\right|\) có hai số lẻ và hai số chẵn.
\(\Rightarrow\)Tổng của 4 số là 1 số chẵn
Mà 2013 là 1 số lẻ
\(\Rightarrow\)Không có giá trị x thỏa mãn
Vậy không có giá trị x thỏa mãn