Question

Chứng minh rằng trong một tam giác cân, độ dài đoạn thẳng nối đỉnh đối diện với đáy và một điểm bất kì của cạnh đáy nhỏ hơn hoặc bằng độ dài của cạnh bên ?

Answer 1

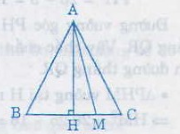
Giả sử ∆ABC cân tại A, M là điểm thuộc cạnh đáy BC, ta chứng minh AM ≤ AB;

AM ≤ AC

+ Nếu M ≡ A hoặc M ≡ B ( Kí hiệu đọc là trùng với) thì AM = AB, AM = AC.

+ Nếu M nằm giữa B và C; ( M ≢ B , C). Gọi H là trung điểm của BC, mà ∆ABC cân tại A nên AH ⊥ BC

+ Nếu M ≡ H => AM ⊥ BC => AM < AB và AM < AC

+ Nếu M ≢ K giả sử M nằm giữa H và C=> MH < CH

Vì MN và CH là hình chiếu MA và CA trên đường BC nên MA < CA => MA < BA

Chứng minh tương tự nếu M nằm giữa H và B thì MA < AB, MA < AC

Vậy mọi giá trị của M trên cạnh đáy BC thì AM ≤ AB, AM ≤ AC

Answer 2

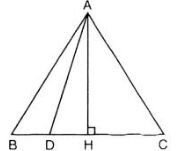
Xét tam giác ABC cân tại A. Gọi D là điểm bất kì của cạnh đáy BC. Kẻ đường cao AH. Ta có:

- Nếu D ≡ B hoặc C thì AD = AB = AC

- Nếu D ≡ H thì AD < AB (hoặc AC)

- Nếu D không trùng B, C, và H, giả sử D nằm giữa D và H thì trong tam giác ABH có BH và DH lần lượt là hình chiếu của AB và AD.

Vì HD < HB nên AD < AB