\(4cos^4x-2cos2x-\frac{1}{2}cos4x=4\left(\frac{cos2x+1}{2}\right)^2-2cos2x-\frac{1}{2}\left(2cos^22x-1\right)\)
\(=cos^22x+2cos2x+1-2cos2x-cos^22x+\frac{1}{2}\)
\(=1+\frac{1}{2}=\frac{3}{2}\)
\(4cos^4x-2cos2x-\frac{1}{2}cos4x=4\left(\frac{cos2x+1}{2}\right)^2-2cos2x-\frac{1}{2}\left(2cos^22x-1\right)\)
\(=cos^22x+2cos2x+1-2cos2x-cos^22x+\frac{1}{2}\)
\(=1+\frac{1}{2}=\frac{3}{2}\)
Chứng minh đẳng thức: \(\dfrac{tan\left(\alpha-\dfrac{\pi}{2}\right).cos\left(\dfrac{3\pi}{2}+\alpha\right)-sin^3\left(\dfrac{7\pi}{2}-\alpha\right)}{cos\left(\alpha-\dfrac{\pi}{2}\right).tan\left(\dfrac{3\pi}{2}+\alpha\right)}=sin^2\alpha\)
Chứng minh đẳng thức sau
\(\dfrac{cos^3x-cos3x}{cosx} + \dfrac{sin^3x+sin3x}{sinx} = 3\)
Chứng minh đẳng thức sau
Sin^2x-tan^2× = tan^6x.(cos^2x-cot^2x)
Chứng minh đẳng thức sau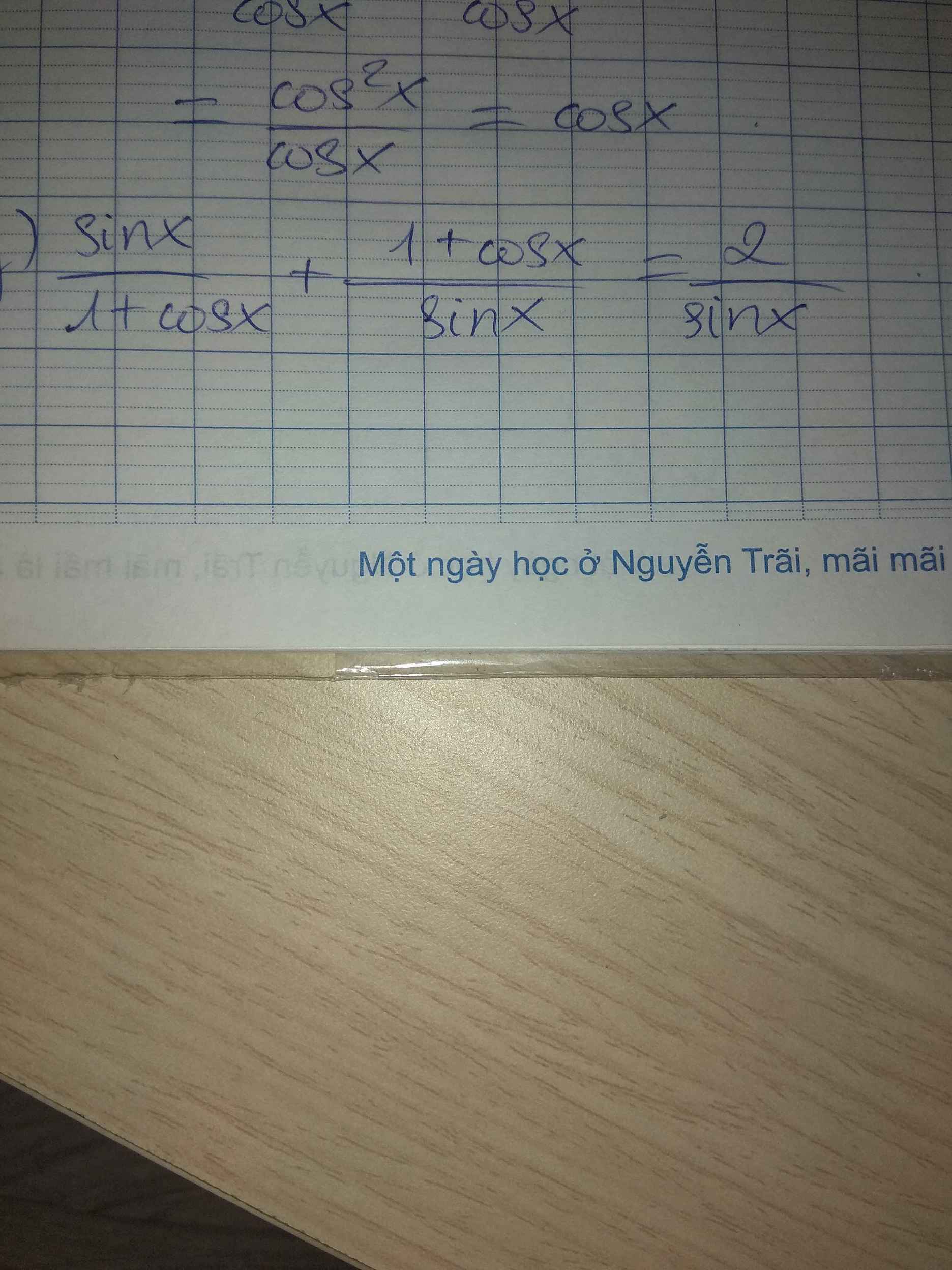
Chứng minh đẳng thức sau: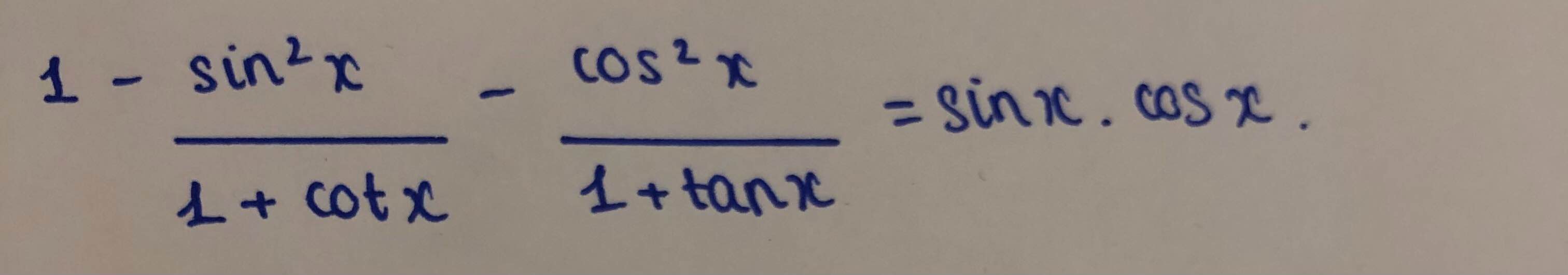
Chứng minh đẳng thức sau: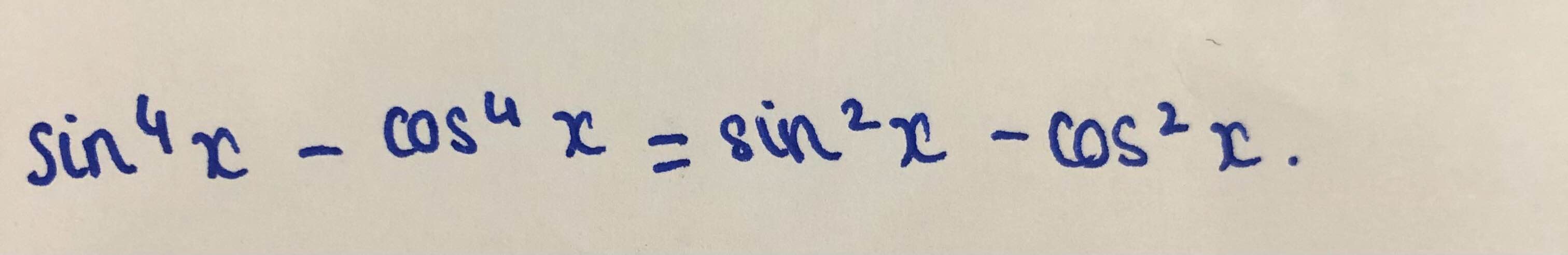
rút gọn biểu thức sau
P=sin2x + sin2(\(\dfrac{pi}{3}-x\)) =sinx*sin(\(\dfrac{pi}{3}-x\))
Chứng minh đẳng thức:
2\(\left(\sin^6\alpha+\cos^6\alpha\right)+1=3\left(\sin^4\alpha+\cos^4\alpha\right)\)
Chứng minh đẳng thức sau: Tanx/sinx - sinx/cotx = cosx