\(A=180^0-\left(B+C\right)=80^0\)
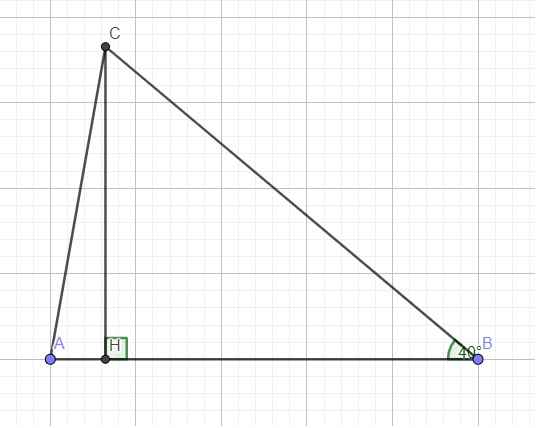
Kẻ đường cao CH ứng với AB, do A và B đều là góc nhọn nên H nằm giữa A và B
Trong tam giác vuông ACH:
\(cotA=\dfrac{AH}{CH}\Rightarrow AH=CH.cotA\)
Trong tam giác vuông CBH:
\(cotB=\dfrac{BH}{CH}\Rightarrow BH=CH.cotB\)
\(\Rightarrow AH+BH=CH\left(cotA+cotB\right)\)
\(\Rightarrow AB=CH.\left(cotA+cotB\right)\)
\(\Rightarrow CH=\dfrac{AB}{cotA+cotB}\)
Trong tam giác vuông ACH:
\(sinA=\dfrac{CH}{AC}\Rightarrow AC=\dfrac{CH}{sinA}=\dfrac{AB}{sinA\left(cotA+cotB\right)}=\dfrac{10}{sin80^0\left(cot80^0+cot40^0\right)}\approx7,42\left(cm\right)\)
Trong tam giác vuông BCH:
\(sinB=\dfrac{CH}{BC}\Rightarrow BC=\dfrac{CH}{sinB}=\dfrac{AB}{sinB\left(cotA+cotB\right)}\approx11,37\left(cm\right)\)