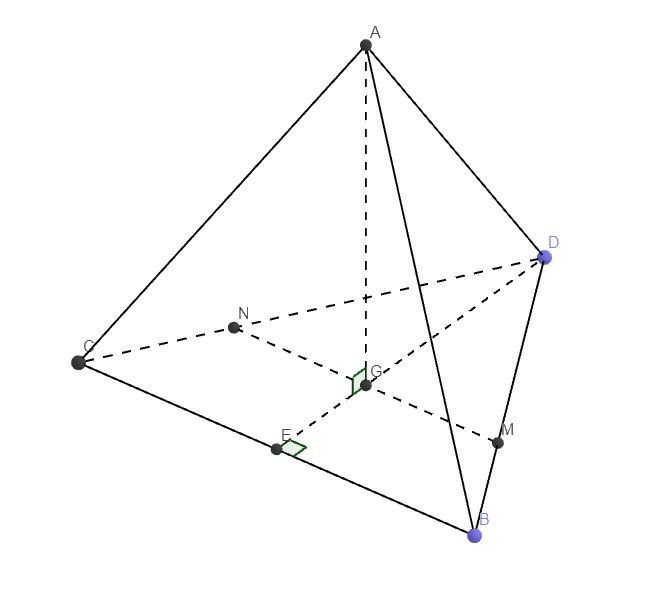
ABCD là tứ diện đều \(\Rightarrow AG\perp\left(BCD\right)\Rightarrow AG\perp DG\)
Gọi E là trung điểm BC, do G là trọng tâm BCD nên theo tính chất trọng tâm
\(\dfrac{DG}{DE}=\dfrac{2}{3}\)
Qua G kẻ đường thẳng song song BC cắt BD và CD tại M và N
Ta có: \(DE=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều) \(\Rightarrow DG=\dfrac{2}{3}DE=\dfrac{a\sqrt{3}}{3}\)
Pitago tam giác vuông ADG: \(AG=\sqrt{AD^2-DG^2}=\sqrt{a^2-\left(\dfrac{a\sqrt{3}}{3}\right)^2}=\dfrac{a\sqrt{6}}{3}\)
Định lý talet: \(\dfrac{GN}{CE}=\dfrac{DG}{DE}=\dfrac{2}{3}\Rightarrow GN=\dfrac{2}{3}CE=\dfrac{2}{3}.\dfrac{a}{2}=\dfrac{a}{3}\)
\(\Rightarrow MN=2GN=\dfrac{2a}{3}\)
\(S_{AMN}=\dfrac{1}{2}AG.MN=\dfrac{a^2\sqrt{6}}{9}\)