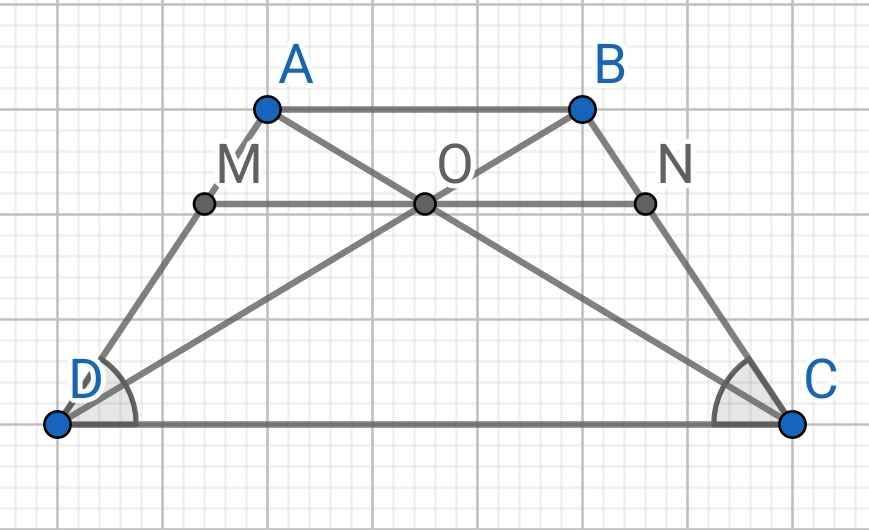
 a) Do ABCD là hình thang cân
a) Do ABCD là hình thang cân
⇒ AD = BC (hai cạnh bên)
∠ADC = ∠BCD (hai góc kề đáy CD)
Xét ∆ADC và ∆BCD có:
AD = BC (cmt)
∠ADC = ∠BCD (cmt)
CD chung
⇒ ∆ADC = ∆BCD (c-g-c)
⇒ ∠ACD = ∠BDC (hai góc tương ứng)
b) Do MN // AB // CD
⇒ ON // AB // CD
Do CD // ON (cmt)
⇒ ∠ACD = ∠NOC (so le trong)
Do CD // AB (gt)
⇒ ∠BDC = ∠ABD (so le trong)
Do AB // ON (cmt)
⇒ ∠ABD = ∠BON (so le trong)
c) Do ∠ACD = ∠NOC (cmt)
∠ACD = ∠BDC (cmt)
⇒ ∠NOC = ∠BDC
Mà ∠BDC = ∠ABD (cmt)
⇒ ∠NOC = ∠ABD
Lại có ∠ABD = ∠BON (cmt)
⇒ ∠NOC = ∠BON
Vậy ON là tia phân giác của ∠BOC













