Sửa đề: DE vuông góc với MP tại F
a) Xét tứ giác MEDF có
\(\widehat{EMF}=90^0\)(\(\widehat{NMP}=90^0\), E∈MN, F∈MP)
\(\widehat{DEM}=90^0\)(DE⊥MN)
\(\widehat{DFM}=90^0\)(DF⊥MP)
Do đó: MEDF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
Sửa đề: DE vuông góc với MP tại F
a) Xét tứ giác MEDF có
\(\widehat{EMF}=90^0\)(\(\widehat{NMP}=90^0\), E∈MN, F∈MP)
\(\widehat{DEM}=90^0\)(DE⊥MN)
\(\widehat{DFM}=90^0\)(DF⊥MP)
Do đó: MEDF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
Cho tam giác MNP vuông tại N, trung tuyến NK. từ K kẻ KE vuông góc với MN, KF vuống góc với NP (E thuộc MN, F thuộc NP).
a) Hỏi tứ giác NEKF là hình gì? Vì sao?
b) Cho MN= 6cm, NP= 8c. Tính độ dài đoạn thẳng EF?
c) Tìm điều kiện của tam giác vuông MNP để tứ giác NEKF là hình vuông?
Cho tam giác MNP vuông tại M , đường cao MH . Gọi D,E là chân đường vuông góc hạ từ H xuống MN và MP
a) Chứng minh tứ giác MDHE là hình chữ nhật
b) Gọi A là trung điểm của HP . Chứng minh tam giác DEA vuông
c) T am giác MNP cần thêm điều kiện gì để DE = 2EA
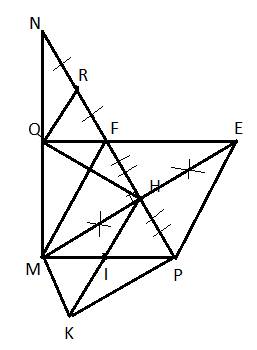
tam giác MNP vuông tại M (MN>MP) đường cao MH. I là trung điểm MP, K đối xứng H qua I, trên tia HN lấy F sao cho HP=HF, E đối xứng M qua H, FQ vuông góc MN (Q ϵ MN), lấy R trung điểm FN
CM: QH vuông góc với QR
Cho tam giác ABC cân tại A, Đường cao BH. Lấy điểm M trên cạnh BC vẽ MD vuông góc vs AC(tại D), MK vuông góc với AB( tại K). Gọi E là điểm đối xứng với K qua BC. a) chứng minh góc BKM bằng góc CMD. Từ đó chứng minh EMD thẳng hàng. b) tứ giác BEDH là hình gì. c)chứng minh MK+MD=BH
Cho tam giác MNP vuông góc tại M, kẻ đường trung tuyến MA. Gọi D là trung điểm của MN, E đối xứng A qua D
a) CMR: E đối xứng A qua MN
b) Tứ giác MENA là hình gì? Vì sao?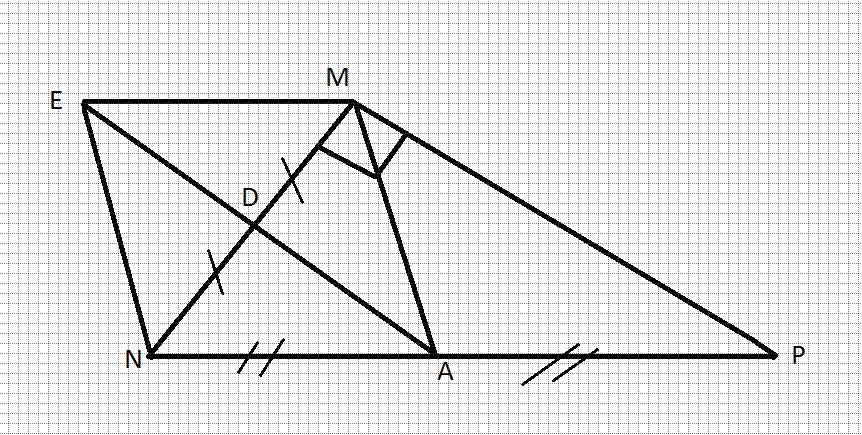
Cho hình vuông ABCD, I là một điểm di động trên cạnh CD. Gọi O là giao điểm AC và BD. Qua I vẽ đường thẳng song song với AC, cắt BD và AD lần lượt ở E và M. Qua I kẻ đường thẳng vuông góc với AC tại K và Cắt BC tại N.
a) Tứ giác EOKI là hình gì ?
b) Chứng minh rằng M , O , N thẳng hàng.
c) Chứng minh rằng I di động trên cạnh CD thì chu vi của EOKI không đổi .
Cho hình vuông ABCD,trên BC lấy điểm M ( M không thuộc B,C).Gọi E là giao điểm của AM với CD. Từ A kẻ đường thẳng vuông góc với AM, cắt DC tại F a,CMR: AF bình =FD.FE b,Tam giác AFM vuông cân tại A c,1/AF bình+1/AE bình không đổi khi M di chuyển trên BC d,Từ C kẻ CK vuông góc AF.Tính FAD
Cho tam giác ABC vuông tại A (AB < AC).Gọi I là trung điểm của cạnh BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N.
a) Tứ giác AMIN là hình gì?
b) Gọi D là điểm đối xứng của I qua N. Chứng minh tứ giác ADCI là hình thoi.
c) Tìm điều kiện của tam giác ABC để tứ giác AMIN là hình vuông . Khi đó tứ giác AICD là hình gì?
d) Đường thẳng BN cắt cạnh DC tại K. Chứng minh:\(\dfrac{DK}{DC}\)=\(\dfrac{1}{3}\)