a)xét tam giác DEH và tam giác DFH có:
EH=FH ( gt)
góc DHE=góc DHF ( vì tam giác DEF cân tại D)
DH:cạnh chung
Do đó: tam giác DEH=tam giác DFH(c-g-c)
a)xét tam giác DEH và tam giác DFH có:
EH=FH ( gt)
góc DHE=góc DHF ( vì tam giác DEF cân tại D)
DH:cạnh chung
Do đó: tam giác DEH=tam giác DFH(c-g-c)
cho tam giác cân DEF (DE=DF).Gọi N và M lần lượt là trung điểm của DE và DF,kẻ DH vuông góc với EF tại H
a) CM HE=HF
b) giả sử DE=DF=5cm,EF=8cm.Tính độ dài đoạn DH
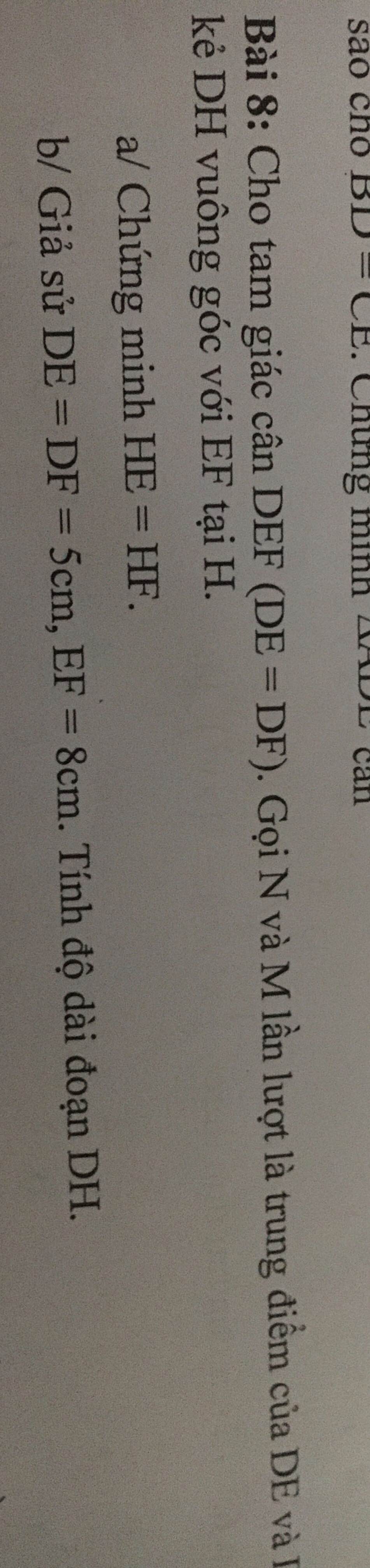
Cho tam giác MNP cân tại M có M<90°,từ M kẻ MH vuông góc với NP(H thuộc NP)
a) chứng minh tam giác MNH = tam giác MPH
b) tính độ dài cạnh MN, biết MH = 4cm và NH = 3cm
c) kẻ ND vuông góc với MP tại D,PE vuông góc với MN tại E. Gọi I là giao điểm của ND và PE.chứng minh MI là phân giác của góc NMP
d) chứng minh 3 điểm M,I,H thẳng hàng
Ghi đầy đủ mà nó hiện lên có 1 khúc,khóc ẻ
Cho tam giác ABC vuông tại A có AB=5cm;AC=12cm.Tia phân giác của góc ABC cắt AC tại D.Từ D kẻ DH vuông góc với BC tại H và DH cắt AB tại K. Chứng minh tam giác BKC cân và B,G,D thẳng hàng ( với G là trọng tâm của tam giác BKC.
Cho tam giác ABC cân tại A .Kẻ BE vuông góc AC tại A , CD vuông góc AB tại D
A,C/M be =Cd
b,c/m tam giác ade là tam giác cân
c,c/m DE//BC
cho tam giác ABC cân tại A (A < 90 độ) kẻ BĐ vuông góc AC tại D.kẻ CE vuông góc AB tại E
a) C/m tam giác ADE cân
b)C/m DE // BC gọi I là giao điểm của BĐ và C/m IB=IC
(Ai giúp mik cần gấp cảm ơn mọi người)
cho tam giác DEF cân tại D,gọi M là trung điểm EF
a) chứng minh tam giác DEM = tam giác DFM , từ đó chứng minh DM vuông góc EF
b)trên tia đối tia ED lấy điểm K,tia đối của tia FD lấy điểm H sao cho EK=FH.chứng minh tam giác DHK là tam giác cân
c) chứng minh EF // HK
d) gọi I là trung điểm HK .chứng minh D,M,I thẳng hàng
e) chứng minh tam giác HFI = tam giác KEI , từ đó chứng minh tam giác IEF là tam giác cân
f) gọi M là trung điểm EK trên tia đối tia MI lấy điểm N sao cho MI=MN ,chứng minh E,F,N thẳng hàng
cho tam giác ABC cân tại A,gọi M là trung điểm của BC
a)chứng minh tam giác ABM = tam giác Acm
b)kẻ MD vuông góc với AB tại D
kẻ ME vuông góc với HC.Chứng minh tam giác BMD =tam giác CDE
c)hỏi tam giác ADE là tam giác gì?Vì sao?
giúp mình làm câu c với ạaaa