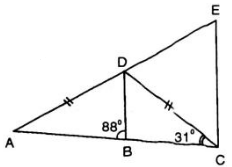
Hướng dẫn làm bài:
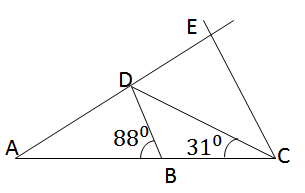
a)∆ADC cân tại D, có ˆADC=310=>ˆADC=1800−2.^CADC^=310=>ADC^=1800−2.C^
=> ˆADC=1800−620=1180ADC^=1800−620=1180
+∆ADB có ^A=310,ˆABD=880A^=310,ABD^=880
=> ˆADB=1800−(310+880)ADB^=1800−(310+880)
Hay ˆADB=610ADB^=610
+BD //CE
=> ˆDEC=ˆADB=610DEC^=ADB^=610 (đồng vị)
b) ˆEDCEDC^ là góc ngoài ∆ADC cân tại D
=> ˆEDC=2.^C=620EDC^=2.C^=620
∆DEC có ^E=610;^D=620=>ˆDCE=570E^=610;D^=620=>DCE^=570
Vì 570<610<620=>DE<DC<CE570<610<620=>DE<DC<CE
Vậy CE là cạnh lớn nhất.