Question

cho tam giác abc vuông tại a trung tuyến am biết BC bằng 10,AC bằng 8  diện tính tích ABM và chu vi AMC

Answer 1

\(AB=\sqrt{10^2-8^2}=6\left(cm\right)\)

\(S_{ABC}=\dfrac{1}{2}\cdot6\cdot8=24\left(cm^2\right)\)

Kẻ đường cao AH

\(S_{ABM}=\dfrac{1}{2}\cdot AH\cdot BM\)

S_ACM=1/2*AH*CM

mà BM=CM

nên \(S_{ABM}=S_{ACM}=\dfrac{24}{2}=12\left(cm^2\right)\)

MA=CB/2=5cm

C_AMC=5+5+8=18(cm)

Answer 2

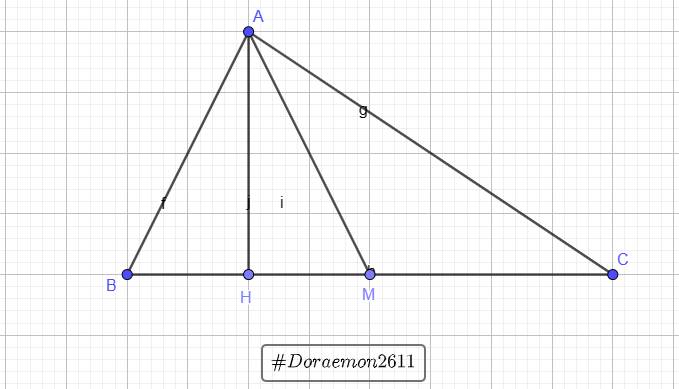
`@` Xét `\triangle ABC` vuông tại `A` có: `AB=\sqrt{BC^2-AC^2}=6`

Gọi `AH` là đường cao của `\triangle ABC` vuông tại `A`

   `=>1/[AH^2]=1/[AB^2]+1/[AC^2]=>AH=24/5`

  Diện tích `\triangle ABM` có `AH` là đường cao là:

  `S_[\triangle ABM]=1/2AH.BM=1/2AH. 1/2BC=1/2 . 24/5 . 1/2 .10=12` (đvdt)

`@` Vì `AM` là đường trung tuyến của `\triangle ABC` vuông tại `A`

   `=>AM=1/2BC=1/2 .10=5`

Chu vi `\triangle AMC` là: `C_[\triangle AMC]=AM+MC+AC=5+5+8=18` (đvđd)