Sửa đề:
Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BA = BE. BD là tia phân giác của góc ABC, AH vuông góc với BC. Chứng minh:
a, Tam giác ABD = tam giác EBD
b, AH // DE
Giải
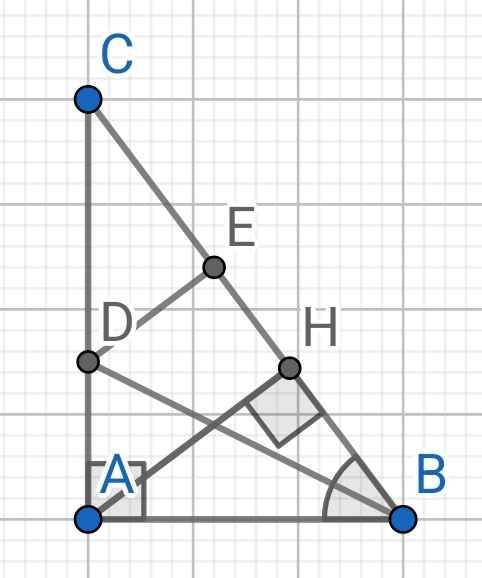 a) Do BD là tia phân giác của ∠ABC (gt)
a) Do BD là tia phân giác của ∠ABC (gt)
⇒ ∠ABD = ∠CBD
⇒ ∠ABD = ∠EBD
Xét ∆ABD và ∆EBD có:
BD là cạnh chung
∠ABD = ∠EBD (cmt)
BA = BE (gt)
⇒ ∆ABD = ∆EBD (c-g-c)
b) Do ∆ABD = ∆EBD (cmt)
⇒ ∠BAD = ∠BED (hai góc tương ứng)
⇒ ∠BED = 90⁰
⇒ DE ⊥ BC
Mà AH ⊥ BC (gt)
⇒ AH // DE
Để chứng minh a, ta cần chứng minh hai tam giác ABD và EBD có cạnh và góc tương ứng bằng nhau.
Vì tam giác ABC vuông tại A, nên ta có góc ABC = 90 độ. Vì BD là tia phân giác của góc ABC, nên ta có góc ABD = góc DBC.
Vì BA = BE, và góc ABD = góc DBC, nên ta có hai cạnh và góc tương ứng bằng nhau, theo nguyên tắc cạnh-góc-cạnh (SAS), ta có tam giác ABD = tam giác EBD.
Để chứng minh b, ta cần chứng minh hai đường thẳng AH và DE là song song.
Vì tam giác ABC vuông tại A, nên ta có góc ABC = 90 độ. Vì BD là tia phân giác của góc ABC, nên ta có góc ABD = góc DBC.
Vì tam giác ABD = tam giác EBD (đã chứng minh ở câu a), nên ta có góc ADB = góc EDB.
Vì góc ADB = góc EDB và góc ABD = góc DBC, nên theo nguyên tắc góc tương đương, ta có AH // DE.
Vậy, ta đã chứng minh được cả hai phần a và b.














