Bài 1: Phương trình bậc nhất hai ẩn
Các câu hỏi tương tự
Cho ΔABC cân tại A (với AB BC) nội tiếp đường tròn (O). Tiếp tuyến tại B và C của đường tròn lần lượt cắt tia AC và tia AB tại D và E. Hãy a) Chứng minh: b) Chứng minh tứ giác BCDE nội tiếp. c) Chứng minh: BC // DE
Đọc tiếp
Cho ΔABC cân tại A (với AB > BC) nội tiếp đường tròn (O). Tiếp tuyến tại B và C của đường tròn lần lượt cắt tia AC và tia AB tại D và E. Hãy
a) Chứng minh:
b) Chứng minh tứ giác BCDE nội tiếp.
c) Chứng minh: BC // DE
Lấy điểm M thuộc nửa đường tròn đường kính AB. vẽ tiếp tuyến tại A của nủa đường tròn. vẽ MH vuông góc với tiếp tuyến đó tại H. So sánh MAH và MBh, chứng minh MH.AB=MA2
Bài 1: Cho tam giác nhọn ABC nội tiếp đường tròn tâm O em O bán kính 4 cm có đường cao AD và OE cắt nhau tại H
a) chứng minh minh tứ giác BEHD nội tiếp
b) Gọi K là giao điểm của tia AD và (O). Chứng minh CB là tia phân giác góc KCE
c) Tính độ dài cung nhỏ AC khi góc ABC 50 độ
Bài 2: Cho PT bậc 2 x2+2x+m-20
a) Tìm m để pt có 2 nghiệm phân biệt
b) Tìm m để PT có 2 nghiệm x1 và x2 thỏa mãn x31+x32-21
Giúp mình với, mình cảm ơn nhé.
Đọc tiếp
Bài 1: Cho tam giác nhọn ABC nội tiếp đường tròn tâm O em O bán kính 4 cm có đường cao AD và OE cắt nhau tại H
a) chứng minh minh tứ giác BEHD nội tiếp
b) Gọi K là giao điểm của tia AD và (O). Chứng minh CB là tia phân giác góc KCE
c) Tính độ dài cung nhỏ AC khi góc ABC = 50 độ
Bài 2: Cho PT bậc 2 x2+2x+m-2=0
a) Tìm m để pt có 2 nghiệm phân biệt
b) Tìm m để PT có 2 nghiệm x1 và x2 thỏa mãn x31+x32=-21
Giúp mình với, mình cảm ơn nhé.
giúp mình vs ah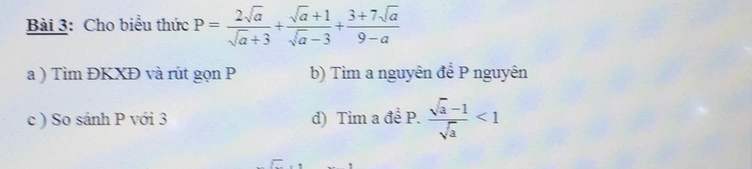
cho một tam giác có đường cao với độ dài bằng một nửa độ dài cạnh đáy thương ứng . nếu tăng chiều cao thêm 2 m và cạnh tương ứng tăng thêm 6m thì được 1 tam giác có diện tích gấp đôi diện tích ban đầu . tính diện tích của tam giác ban đầu
Cho đường tròn (O). Từ điểm P bên ngoài đường tròn vẽ cát tuyến PAB và hai tiếp tuyến PM,PN với (O) (M thuộc cung nhỏ AB). Lấy D là điểm chính giữa của cung lớn AB, DM cắt AB tại I. a) Chứng minh: PM = PI b) IA . NB = IB . NA c) Trên cát tuyến PAB lấy PK = PN. Chứng minh NK là tia phân giác của góc ANB.
Cho mặt phẳng Oxy :(P) y=2x2 và y=mx+1
Tìm m để SAOB =\(\dfrac{3m}{2}\)
(biết d cắt P tại 2 điểm phân biệt A và B)
Giúp mk cần gấp
Cho a,b,c >0 thoả mãn a+b+c=1. CM \(\frac{1}{a^2+b^2+c^2}+\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}\ge30\)
HELP ME
a) Giải hệ phương trình: left{{}begin{matrix}dfrac{3x}{x+1}-dfrac{2}{y+4}4dfrac{2x}{x+1}-dfrac{5}{y+4}9end{matrix}right.
b)Giải phương trình: sqrt[3]{2+x}+sqrt[3]{5-x}1
c) Cho a, b, c 0 thỏa mãn biểu thức a+b+c1
Chứng minh rằng: sqrt{a+bc}+sqrt{b+ac}+sqrt{c+ab}le2
Mn giúp mình với ạ, mk cần gấp lắm a~. Cảm ơn mn nhiều
Đọc tiếp
a) Giải hệ phương trình: \(\left\{{}\begin{matrix}\dfrac{3x}{x+1}-\dfrac{2}{y+4}=4\\\dfrac{2x}{x+1}-\dfrac{5}{y+4}=9\end{matrix}\right.\)
b)Giải phương trình: \(\sqrt[3]{2+x}+\sqrt[3]{5-x}=1\)
c) Cho a, b, c > 0 thỏa mãn biểu thức a+b+c=1
Chứng minh rằng: \(\sqrt{a+bc}+\sqrt{b+ac}+\sqrt{c+ab}\le2\)
Mn giúp mình với ạ, mk cần gấp lắm a~. Cảm ơn mn nhiều










