Bài 1: Định lý Talet trong tam giác
Các câu hỏi tương tự
Cho tam giác ABC. Từ điểm D trên cạnh BC, kẻ các đường thẳng song song với các cạnh AB và AC, chúng cắt các cạnh AC và AB theo thứ tự tại F và E (h.4)
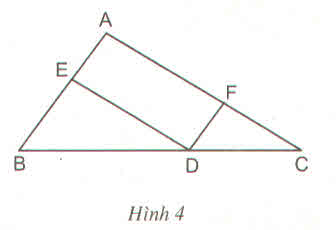
Chứng minh rằng :
\(\dfrac{AE}{AB}+\dfrac{AF}{AC}=1\)
Bài 2: Cho tam giác ABC. Từ điểm D trên cạnh BC, kẻ các đường thẳng song song với các cạnh AB và AC, chúng cắt các cạnh AC và AB theo thứ tự tại F và E. Chứng minh rằng: AE trên AB+À trên AC =1
giúp mik với mik cần gấp thanks nhiều![]()
Cho ∆𝐴𝐵𝐶 và điểm D thuộc BC sao cho \(\dfrac{BD}{DC}\) = \(\dfrac{1}{2}\). Từ D kẻ các đường thẳng // với AB, AC lần lượt tại F và E.
a, So sánh \(\dfrac{AF}{AB}\) và \(\dfrac{AE}{AC}\)
b, C/m EF // trung tuyến BI của \(\Delta\)ABC
Cho tam giác ABC ,I là điểm thuộc D thuộc tam giác đó AI,BI,CI cắt BC,CA,AD tại M,N,P.CMR:
\\(\dfrac{MB}{MC}.\dfrac{NC}{NA}\dfrac{DA}{DB}\)
Cho tam giác ABC, điểm D nằm trên cạnh AB sao cho AD = 2DB, lấy E trên AC sao cho DE // BC. Biết AE +AC =15cm.
a) Tính \(\dfrac{AE}{AC}\)
b) Tính AE, AC, EC
cho tam giác ABC. Một đường thẳng song song với BC cắt cạnh AB và AC theo thứ tự ở D và E.
a) Biết \(\frac{AE}{EC}\)=\(\frac{3}{4}\), BC = 28cm. Tính độ dài DE.
b) Biết \(\frac{AD}{BD}\)=\(\frac{EC}{AE}\),CMR D,E theo thứ tự là trung điểm của AB, AC
Cho tam giác ABC, một đường thẳng // với BC cắt AB và AC theo thứ tự ở D và E. Qua E kẻ đường thẳng // với CD, cắt AB ở F. CM hệ thức : AD2=AB.AF
Cho tam giác ABC , từ điểm D trên cạnh BC kẻ các đường thẳng song song với các cạnh AB và AC , chúng cắt các cạnh AB và AC theo thứ tự tại E và F . Chứng minh rằng AF/AB + AE/AC = 1








