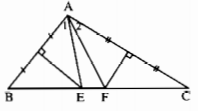
Vì E thuộc đường trung trực của đoạn thẳng AB nên EA = EB, hay tam giác EAB cân tại đỉnh E. Suy ra \(\widehat{B}=\widehat{A_1}\). Tương tự, có \(\widehat{C}=\widehat{A_2}\). Ta có:
\(\widehat{EAF}=\widehat{A}-\left(\widehat{A_1}+\widehat{A_2}\right)=\widehat{A}-\left(\widehat{B}+\widehat{C}\right)\)
Mặt khác
\(\widehat{B}+\widehat{C}=180^0-\widehat{A}=180^0-100^0=80^0\)









