BC: dùng Pitago là ra =20cm
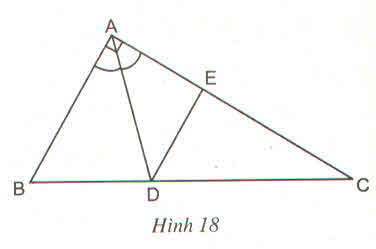
-Vì AD là tia ph/giác nên \(\frac{AB}{AC}=\frac{BD}{CD}=\frac{12}{16}=\frac{3}{4}\Rightarrow BD=\frac{3}{4}CD\)
BD+CD=BC\(\Leftrightarrow CD+\frac{3}{4}CD=20\Leftrightarrow\frac{7}{4}CD=20\Rightarrow CD=\frac{80}{7}\)\(\Rightarrow BD=20-\frac{80}{7}=\frac{60}{7}\)
-ED//AB nên \(\frac{DE}{AB}=\frac{CD}{BC}=\frac{4}{7}\left(CMT\right)\Rightarrow DE=\frac{12.4}{7}=\frac{48}{7}\)
Xét \(\Delta AHB\&\Delta CHA\) vuông có
\(\widehat{BAH}=\widehat{ACH}\)( cộng với góc HAC đều =90)
Suy ra AHB đồng dạng CHA(1)
\(\Rightarrow\left\{{}\begin{matrix}\frac{AH}{HC}=\frac{AB}{AC}=\frac{3}{4}\\\frac{AH}{HB}=\frac{AC}{AB}=\frac{4}{3}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}4AH=3HC\\3AH=4HB\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}16AH=12HC\left(2\right)\\9AH=12HB\left(3\right)\end{matrix}\right.\)
Cộng (2) và (3) được 25AH=12HC+12HB=12BC=12.20.Giải ra AH
Có \(\frac{AH}{HC}=\frac{AB}{AC}=\frac{3}{4}\Rightarrow HC=\frac{4AH}{3}=\frac{4.\frac{48}{5}}{3}=12,8\)
HB<BD nên H nằm giữa B,D suy ra HD=BD-HB=....
\(Công thức tính đường cao trong tam giác vuông Giả sử có tam giác vuông ABC vuông tại A như hình sau: Công thức tính đường cao trong tam giác vuông Công thức tính cạnh và đường cao trong tam giác vuông: 1. a 2 = b 2 + c 2 2. b 2 = a . b ′ và c 2 = a . c ′ 3. ah = bc 4. h 2 = b ′ . c ′ 5. 1 h 2 = 1 b 2 + 1 c 2 Trong đó: a, b, c lần lượt là các cạnh của tam giác vuông như hình trên; b’ là đường chiếu của cạnh b trên cạnh huyền; c’ là đường chiếu của cạnh c trên cạnh huyền; h là chiều cao của tam giác vuông được kẻ từ đỉnh góc vuông A xuống cạnh huyền BC. Như vậy các bạn có thể dựa vào các công thức cạnh và đường cao trong tam giác vuông ở trên để giải quyết các bài toán.\)