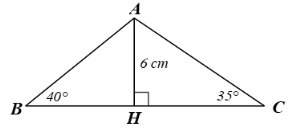
Xét tam giác \(ABH\) vuông tại \(H\), ta có:
+) \(AB = \frac{{AH}}{{\sin 40^\circ }} = \frac{6}{{\sin 40^\circ }} \approx 9,3\left( {cm} \right)\).
+) \(BH = \frac{{AH}}{{\tan 40^\circ }} = \frac{6}{{\tan 40^\circ }} \approx 7,2\left( {cm} \right)\).
Xét tam giác \(AHC\) vuông tại \(H\), ta có:
+) \(AC = \frac{{AH}}{{\sin 35^\circ }} = \frac{6}{{\sin 35^\circ }} \approx 10,5\left( {cm} \right)\).
+) \(CH = \frac{{AH}}{{\tan 35^\circ }} = \frac{6}{{\tan 35^\circ }} \approx 8,6\left( {cm} \right)\).
Ta có: \(BC = BH + HC \approx 7,2 + 8,6 \approx 15,8\left( {cm} \right)\).
Đúng 0
Bình luận (0)


