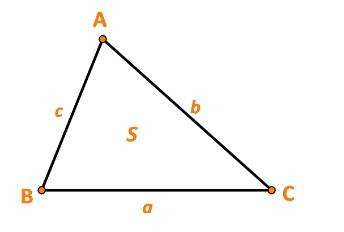
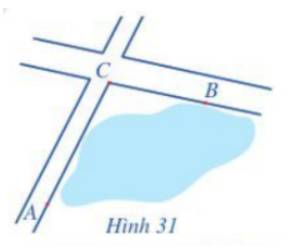
Ta có: \(a = BC = 20;\;b = AC = 15;\;c = AB = 12.\)
a) Áp dụng định lí cosin trong tam giác ABC, ta có:
\(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\;\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\)
\( \Rightarrow \cos A = \frac{{{{15}^2} + {{12}^2} - {{20}^2}}}{{2.15.12}};\;\cos B = \frac{{{{20}^2} + {{12}^2} - {{15}^2}}}{{2.20.12}}\)
\( \Rightarrow \cos A = - \frac{{31}}{{360}};\;\cos B = \frac{{319}}{{480}}\)
\( \Rightarrow \widehat A = 94,{9^o};\;\widehat B = 48,{3^o}\)
\( \Rightarrow \widehat C = {180^o} - \left( {94,{9^o} + 48,{3^o}} \right) = 36,{8^o}\)
b)
Diện tích tam giác ABC là: \(S = \frac{1}{2}.bc.\sin A = \frac{1}{2}.15.12.\sin 94,{9^o} \approx 89,7.\)