xl vẽ k đc đẹp.
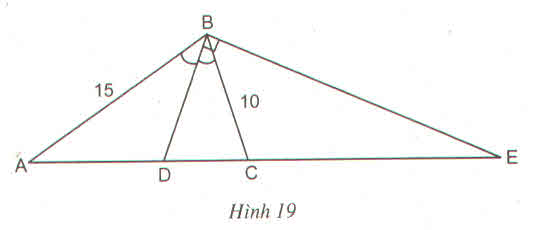
ΔDEC cân . Đặt DE=DC=x thì AD = b-x .Áp dụng hệ quả đ/l Ta-lét ta có:
\(\dfrac{DE}{BC}=\dfrac{AD}{AC}\) hay \(\dfrac{x}{a}=\dfrac{b-x}{b}\) ; \(ax+bx=ab;x=\dfrac{ab}{a+b}=DE\)
\(\Leftrightarrow\dfrac{1}{DE}=\dfrac{a+b}{ab}=\dfrac{1}{a}+\dfrac{1}{b}\)
Lời giải:
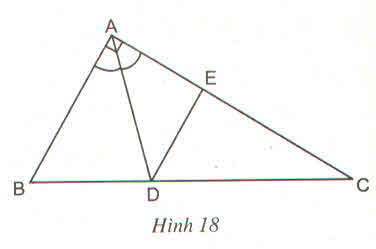
Xét tam giác $ABD$ và $ACE$ có:
$\widehat{A}$ chung
$AB=AC$ (do tam giác $ABC$ cân tại $A$)
$\widehat{ABD}=\frac{1}{2}\widehat{B}=\frac{1}{2}\widehat{C}=\widehat{ACE}$ (do tam giác $ABC$ cân tại $A$)
$\Rightarrow \triangle ABD=\triangle ACE$ (g.c.g)
$\Rightarrow AD=AE$
Mà $AB=AC$ nên $\frac{AE}{AB}=\frac{AD}{AC}$
$\Rightarrow DE\parallel BC$ (Talet đảo)
Áp dụng định lý Talet:
$\frac{DE}{BC}=\frac{AD}{AC}$
Theo tính chất tia phân giác thì:
$\frac{AD}{DC}=\frac{AB}{BC}=\frac{b}{a}$
$\Rightarrow \frac{AD}{AC}=\frac{b}{a+b}$
Do đó: $\frac{DE}{BC}=\frac{b}{a+b}$
$\Rightarrow DE=BC.\frac{b}{a+b}=\frac{ab}{a+b}$