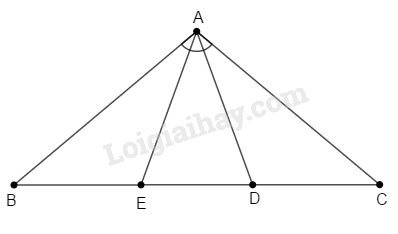
+ Vì \(\Delta ABC\) cân tại \(A\left(gt\right)\)
=> \(\widehat{B}=\widehat{C}\) (tính chất tam giác cân).
=> \(\widehat{B}=\widehat{C}=\frac{180^0-\widehat{A}}{2}\)
=> \(\widehat{B}=\widehat{C}=\frac{180^0-110^0}{2}=\frac{70^0}{2}=35^0.\)
+ Xét \(\Delta ABD\) có:
\(BD=BA\left(gt\right)\)
=> \(\Delta ABD\) cân tại B.
=> \(\widehat{BAD}=\widehat{ADB}\) (tính chất tam giác cân).
=> \(\widehat{BAD}=\widehat{ADB}=\frac{180^0-\widehat{B}}{2}\)
=> \(\widehat{BAD}=\widehat{ADB}=\frac{180^0-35^0}{2}=\frac{145^0}{2}=72,5^0.\)
=> \(\widehat{ADB}=72,5^0\)
Hay \(\widehat{ADE}=72,5^0.\)
+ Xét \(\Delta ACE\) có:
\(CE=CA\left(gt\right)\)
=> \(\Delta ACE\) cân tại C.
=> \(\widehat{CAE}=\widehat{AEC}\) (tính chất tam giác cân).
=> \(\widehat{CAE}=\widehat{AEC}=\frac{180^0-\widehat{C}}{2}\)
=> \(\widehat{CAE}=\widehat{AEC}=\frac{180^0-35^0}{2}=\frac{145^0}{2}=72,5^0.\)
=> \(\widehat{AEC}=72,5^0\)
Hay \(\widehat{AED}=72,5^0.\)
+ Xét \(\Delta ADE\) có:
\(\widehat{DAE}+\widehat{ADE}+\widehat{AED}=180^0\) (định lí tổng 3 góc trong một tam giác).
=> \(\widehat{DAE}+72,5^0+72,5^0=180^0\) => \(\widehat{DAE}+145^0=180^0\) => \(\widehat{DAE}=180^0-145^0\) => \(\widehat{DAE}=35^0.\) Vậy \(\widehat{DAE}=35^0.\) Chúc bạn học tốt!










