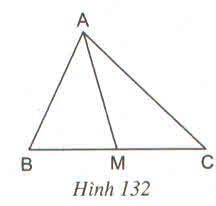
Xét ΔABC có
C',B' lần lượt là trung điểm của AB,AC
nên C'B' là đường trung bình
=>C'B'//BA' và C'B'=BA'
Xét ΔAC'B' và ΔC'BA' có
AC'=C'B
góc AC'B'=góc C'BA'
C'B'=BA'
=>ΔAC'B'=ΔC'BA'
=>\(S_{AB'C'}=S_{BA'C'}\)(1)
Xét tứ giá BC'B'A' có
C'B'//BA'
C'B'=BA'
=>BC'B'A' là hình bình hành
=>A'B'//BC' và A'B'=BC'
Xét ΔA'C'B và ΔCB'A' co
A'C'=CB'
C'B=B'A'
A'B=A'C
=>ΔA'C'B=ΔCB'A'
=>\(S_{BA'C'}=S_{CA'B'}\)(2)
Xét ΔBCA co
A',C' lần lượt là trung điểm của BC,BA
nên A'C' là đường trung bình
=>A'C'//AB' và A'C'=AB'
=>AC'A'B' là hình bình hành
Xét ΔAC'B' và ΔA'B'C' có
AC'=A'B'
C'B' chung
AB'=A'C'
=>ΔAC'B=ΔA'B'C'
=>\(S_{AC'B}=S_{A'B'C'}\)(3)
Từ (1), (2), (3) suy ra ĐPCM