Chương I - Hệ thức lượng trong tam giác vuông
Các câu hỏi tương tự
Cho tam ABC có góc A bằng 90 độ và đường cao AH ( H thuộc BC) kẻ HE và HF lần lượt vuông góc với AB và AC tại E,F
1, chứng minh AEHF là hcn và tính EF , CF
2, tính diện tích tứ giác AEHF
3, tính diện tích tứ giác BEFC
1. Cho tam giác ABC vuông tại A, AB=15cm, AC=20cm.
a) Tính BC, góc B, góc C
b) Phân giác của góc A cắt BC tại E. Tính BE, CE.
c) Từ E kẻ EM lần lượt vuông góc với AB và AC. Hỏi tứ giác AMEN là hình gì? Tính chu vi và diện tích của tứ giác AMEN.
d) Chứng minh: \(\dfrac{1}{AB}+\dfrac{1}{AC}=\dfrac{\sqrt{2}}{AE}\)
Bài 3: Cho ∆ ABC vuông tại A, đường cao AH biết HB=4cm ; HC= 9cm . a) Tính AB và AH. b) Từ HE vuông góc với AB, HF vuông góc với AC Tử giác AEHF là hình gì? Tính EF ?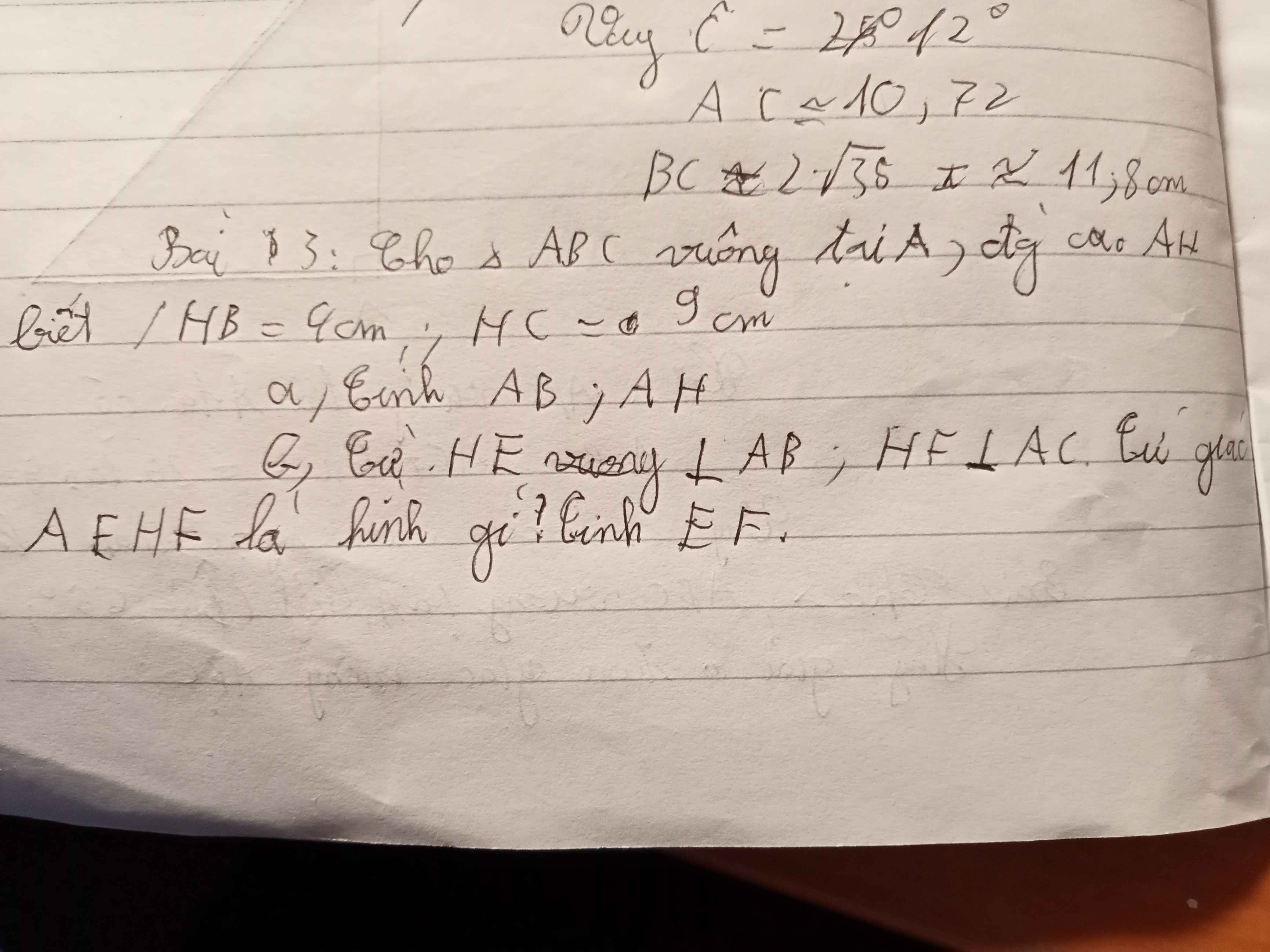
Cho tam giác ABC vuông tại A, đường cao AH, AB=3cm, BC=6cm. 1) Giải tam giác ABC 2) Gọi E, F lần lượt là hình chiếu của H trên cạnh AB và AC. a) Tính độ dài AH và chứng minh: EF=AH b) Tính: EA.EB+AF.FC
3, cho tg ABC vg tại A , AB = 15cm, AC = 20cm.
a, tính BC, góc B, góc C.
b, phân giác của góc A cắt BC tại E. Tính BE, CE.
c, từ E kẻ EM và EN lần lượt vg góc vs AB và AC. Hỏi tứ giác AMEN là hình gì? Tính chu vi và diện tích tứ giác AMEN.
Bài 2: Cho ∆ABC vuông ở A, AH ⊥ BC, AB = 3cm, BC = 6cm.
a) Tính BH, CH, AC, AH và 𝐴̂𝐵𝐶
b) Kẻ HD ⊥ AB, HE ⊥ AC (D thuộc AB; E thuộc AC). Tính BD, so sánh AB.AD và AC.AE.
c) Tính diện tích tứ giác AEHD, diện tích tam giác ACH.
(Diện tích làm tròn đến chữ số thập phân thứ ba).
Cho tam giác ABC vuông tại A đường cao AH, AB=6, BC=10 a) Tính BH, HC, AH, góc BAH. b) Vẽ BD là tia phân giác của tam giác ABH ( D thuộc AC ). Kẻ AK vuông góc với BD tại K. Cmr: BH.BC=BK.BD. c) BD cắt AH tại S. Tính diện tích tứ giác SHCD?
Cho tam giác ABC có AC = 16cm, AB = 12cm, BC = 20cm. Đường cao AH.
a,Chứng minh tam giác ABC vuông.
b,Tính đường cao AH.
c,Từ H vẽ HE vuông góc với AB và HF vuông góc với AC. Tính HE, HF
d,So sánh: tanB và sinB (mình cần nhất câu này thôi 3 câu trên có hay không không quan trọng cảm ơn ae)
Cho tam giác ABC vuông tại A có đường cao AH.
Biết AB = 12 cm, AC = 16 cm.
a) Tính độ dài các đoạn thẳng BC, AH,
BH và CH.
b) Kẻ HE ⊥ AB (E ∈ AB) và HF ⊥ AC
(F ∈ AC). Chứng minh rằng AE.AB =
AF.AC và suy ra tam giác ABC ∼ AFE.










