Nối O với H
Xét đg tròn (O), có:
OK∈ đg kính
K là td của HI (gt)
HI là dây không đi qua tâm
⇒OK⊥HI tại K
⇒HKI=90o
⇒ΔHKI vg tại K
Xét ΔHKI vg tại K, có:
HK2+OK2=OH2(ĐL Pi ta go)
Mà HK=8 cm (K là td của HI)
OH= 10cm (=R)
⇒OK2=36
⇒OK=6 cm (Vì OK>0)
Cho (O;10cm) và dây HI = 16cm. Tính OK = ?
Sẵn tiện cho mìk hỏi nhu xíu cái chỗ ( O; 10cm) là sao mìk ko hỉu đoạn nào 10cm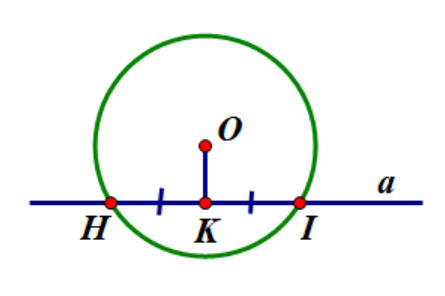
a) Vẽ đồ thị hàm số y = – 2x2
b) Cho đường tròn (O), đường kính AB; P 
(O) sao cho 
(Hình 3). Tính số đo 
c) Một hình trụ có chiều cao bằng 12 cm và diện tích xung quanh là 96
cm2. Hãy tính bán kính của đường tròn đáy đó?
Cho hàm số y= 2x-3 có đồ thị (D)
a) Vẽ đồ thị (D)
b)Tính khoảng cách từ gốc tọa độ đến (D)
c) Tính góc a tạo bởi đường thẳng (D) và trục Ox.(Làm tròn đến phút)
BÀI 1 :Cho parabol y=x^2 và đường thẳng d:y= -2x+m1.
Với m = 3, hãy:a) Vẽ (d) và (P) trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ các giao điểm M và N của (d) và (P).
c) Tính độ dài đoạn thẳng MN.2. Tìm các giá trị của m để:
1) (d) và (P) tiếp xúc nhau.
2) (d) cắt (P) tại hai điểm phân biệt
Bài 2: Cho parabol và đường thẳng
.
1. Với m = 3, hãy:
a) Vẽ (d) và (P) trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ các giao điểm M và N của (d) và (P).
c) Tính độ dài đoạn thẳng MN.
2. Tìm các giá trị của m để:
a) (d) và (P) tiếp xúc nhau.
b) (d) cắt (P) tại hai điểm phân biệt.
Cho hàm số y = -\(\dfrac{3}{2}\)x\(^2\) có đồ thị (P) và y = -2x + \(\dfrac{1}{2}\) có đồ thị (d)
1/ Vẽ (P) và (d) trên cùng một hệ trục tọa độ vuông góc. Xác định tọa độ các giao điểm của (P) và (d).
2/ Tìm tọa độ những điểm trên (P) thỏa tính chât tổng hoành độ và tung độ của điểm đó bằng -4.
Cho phương trình x^2 + 2(m - 3)x + m^2 =0 a. Giải phương trình với m = 0 b. Tìm m pt có hai nghiệm phân biệt. Tính tổng và tích hai nghiệm theo m
Câu 1: a) Cho biết \(a=2+\sqrt{3}\) và \(b=2-\sqrt{3}\). Tính giá trị biểu thức P = a + b - ab
b) Giải hệ phương trình: \(\left\{{}\begin{matrix}3x+y=5\\x-2y=-3\end{matrix}\right.\)
Câu 2: Cho biểu thức: \(P=\left(\dfrac{1}{x-\sqrt{x}}+\dfrac{1}{\sqrt{x}-x}\right):\dfrac{\sqrt{x}}{x-2\sqrt{x}+1}\) (với x>0, x\(\ne\)1)
a) Rút gọn biểu thức P
b) Tìm các giá trị của x để P >\(\dfrac{1}{2}\)
cho A(0;2);B(6;9);C(4;1);D(3;10)
a)C/m tứ giác ABCD là hình chữ nhật
b)Gọi O là giao diểm 2 đường chéo tìm tọa độ điểm O
Cho (O;10cm) và dây HI = 16cm. Tính OK = ?
