Ôn thi vào 10
Các câu hỏi tương tự
cho nửa đường tròn tâm o đường kính ab trên nửa đường tròn lấy điểm c sao cho ca <cb,vẽ ch vuông góc với ab (h thuộc ab).trên cung bc lấy điểm d bất kì (d khác b và c),gọi e là giao diểm của ch và ad.
a)chứng minh tứ giác bdhe nội tiếp đường tròn
b)chứng minh ac bình phương = ae.ad
Cho nửa đường tròn tâm (O), đường kính AB = 2R và điểm M nằm trên đường tròn sao cho AM = R. N là điểm nằm trên cung MB ( N khác M và B). Gọi I là giao điểm của AN và MB. H là hình chiếu vuông góc của A trên AB. Gọi K là giao điểm của AM và BN. C/m: HK là tia phân giác của góc MHN.
cho nửa đường tròn (O) đường kính AB và C là một điểm thuộc nửa đường tròn sao C khác A, B và AC CB . Điểm D nằm trên dây cung BC sao cho widehat{DOC}90^0 E là giao điểm của AD và BC. F là giao điểm của AC và BD.a) chứng minh tứ giác CEDF nội tiếpb) chúng minh FC.FA FD.FBc) Gọi I là trung điểm của FE. Chứng minh rằng IC IC là tiếp tuyến của (O)d) Khi C thay đổi thỏa mãn điều kiện của bài toán thì I thuộc đường tròn cố định nào?
Đọc tiếp
cho nửa đường tròn (O) đường kính AB và C là một điểm thuộc nửa đường tròn sao C khác A, B và AC < CB . Điểm D nằm trên dây cung BC sao cho \(\widehat{DOC}=90^0\) E là giao điểm của AD và BC. F là giao điểm của AC và BD.
a) chứng minh tứ giác CEDF nội tiếp
b) chúng minh FC.FA= FD.FB
c) Gọi I là trung điểm của FE. Chứng minh rằng IC IC là tiếp tuyến của (O)
d) Khi C thay đổi thỏa mãn điều kiện của bài toán thì I thuộc đường tròn cố định nào?
Cho nửa đường tròn đường kính AB. Trên nửa đường tròn lấy C (C khác A, B). Gọi H là hình chiếu của C trên AB. Trên cung CB lấy D (D khác C, B). Hai đường thẳng AD và CH cắt tại E Chứng minh
a) tứ giác BDEH nội tiếp.
b )Chứng minh AC^2 = AE.AD
c ) gọi (O) là đường tròn qua D và tiếp xúc AB tại B ,(O') cắt CB tại F.Chứng minh EF//AB
Bài 2: Cho nửa đường tròn tâm O đường kính AB 2R. Trên cung AB lấy hai điểm C và D sao cho C thuộc cung AD (C và D không trùng A và B). Gọi I là giao điểm của AD và BC. Vẽ IH vuông góc với AB tại H.a) Chứng minh: Tứ giác BDIH nội tiếp được đường tròn.b) Chứng minh DA là tia phân giác của CDH .c) Gọi K là trung điểm của BI. Chứng minh: C, H, K, D cùng thuộc một đường tròn CÓ HÌNH NỮA NHA
Đọc tiếp
Bài 2: Cho nửa đường tròn tâm O đường kính AB = 2R. Trên cung AB lấy hai điểm C và D sao cho C thuộc cung AD (C và D không trùng A và B). Gọi I là giao điểm của AD và BC. Vẽ IH vuông góc với AB tại H.
a) Chứng minh: Tứ giác BDIH nội tiếp được đường tròn.
b) Chứng minh DA là tia phân giác của CDH .
c) Gọi K là trung điểm của BI. Chứng minh: C, H, K, D cùng thuộc một đường tròn CÓ HÌNH NỮA NHA
23 tháng 5 2021 lúc 15:42
Cho tứ giác ABCD có 2 đỉnh B và C trên nửa đường tròn đường kính AD, tâm O. Hai đường chéo AC và BD cắt tại E. Gọi H là hình chiếu vuông góc từ E kẻ xuống AD và I là trung điểm DE. Cmr: a) ABEH và DCEH nội tiếpb) E là tâm đường tròn nội tiếp tam giác BCHc) 5 điểm B,C,I,O,H thuộc đường tròn
Đọc tiếp
Cho tứ giác ABCD có 2 đỉnh B và C trên nửa đường tròn đường kính AD, tâm O. Hai đường chéo AC và BD cắt tại E. Gọi H là hình chiếu vuông góc từ E kẻ xuống AD và I là trung điểm DE. Cmr:
a) ABEH và DCEH nội tiếp
b) E là tâm đường tròn nội tiếp tam giác BCH
c) 5 điểm B,C,I,O,H thuộc đường tròn
23 tháng 6 2021 lúc 16:10
8/75cho đường tròn O đường kính AB , điểm C nằm trên đường tròn (C khác A và B) . gọi M,N lần lượt là điểm chính giữa của cung AC nhỏ và cung BC nhỏ . gọi E là giao điểm của ON và CB . từ N vẽ NK vuông góc AC ( K thuộc AC)A/ chứng minh tứ giác ECKN là hình chữ nhật và suy ra KN là tiếp tuyến tại N của đường tròn OB/ vẽ đường kinh ND của đường tròn O . chứng minh tứ giác KEDA là hình bình hànhC/ gọi I là giao điểm của MN và KO . chứng minh (căn 2) /NI 1/NK + 1/NOthankkkkkkkkkkkkkkkkkkkk
Đọc tiếp
8/75
cho đường tròn O đường kính AB , điểm C nằm trên đường tròn (C khác A và B) . gọi M,N lần lượt là điểm chính giữa của cung AC nhỏ và cung BC nhỏ . gọi E là giao điểm của ON và CB . từ N vẽ NK vuông góc AC ( K thuộc AC)
A/ chứng minh tứ giác ECKN là hình chữ nhật và suy ra KN là tiếp tuyến tại N của đường tròn O
B/ vẽ đường kinh ND của đường tròn O . chứng minh tứ giác KEDA là hình bình hành
C/ gọi I là giao điểm của MN và KO . chứng minh (căn 2) /NI = 1/NK + 1/NO
thankkkkkkkkkkkkkkkkkkkk
Câu 9: (1,0 điểm) Cho đường tròn (O), đường kính AB. Lấy điểm C nằm trên đường tròn (C ≠ A, C ≠ B). Các tiếp tuyến của đường tròn (O) tại A và C cắt nhau tại D. Gọi H là hình chiếu vuông góc của C trên đường thẳng AB. I là giao điểm của BD và CH. Chứng minh rằng CI HI.giúp e với ạ e tra mạng có phần e chưa hiểu lắm
Đọc tiếp
Câu 9: (1,0 điểm) Cho đường tròn (O), đường kính AB. Lấy điểm C nằm trên đường tròn (C ≠ A, C ≠ B). Các tiếp tuyến của đường tròn (O) tại A và C cắt nhau tại D. Gọi H là hình chiếu vuông góc của C trên đường thẳng AB. I là giao điểm của BD và CH. Chứng minh rằng CI = HI.
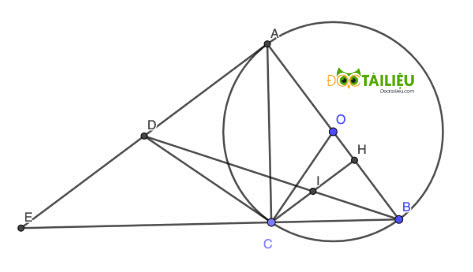
giúp e với ạ e tra mạng có phần e chưa hiểu lắm
cho đường tròn (O;R) đường kính AB. Trên đường tròn (O) lấy hai điểm C và D nằm khác phía AB sao cho AC=AD. Trên cung nhỏ BC lấy điểm M (M khác B,C). Gọi I,K lần lượt là giao điển của CD với AB và AM chứng minh tứ giác IKMB nội tiếp