Cho nửa đường tròn tâm O, đường kính AB = 2R, Ax và By là hai tiếp tuyến vởi nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP cắt By tại N.
a) Chứng minh rằng MON và APB là hai tam giác vuông đồng dạng.
b) Chứng minh \(AM.BN=R^2.\)
c) Tính tỉ số \(\dfrac{S_{MON}}{S_{APB}}\) khi \(AM=\dfrac{R}{2}.\)
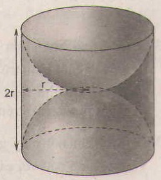
d) Tính thể tích của hình do nửa hình tròn APB quay quanh AB sinh ra.
Giải:
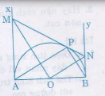
a) Ta có OM, ON lần lượt là tia phân giác cả AOP và BOP
Mà AOP kể bù BOP nên suy ra OM vuông góc với ON.
Vậy ∆MON vuông tại O.
Lại có ∆APB vuông vì có góc vuông (góc nội tiếp chắn nửa cung tròn)
Tứ giác AOPM nội tiếp đường tròn vì có +
= 2v. Nên
=
(cùng chắn cung OP).
Vậy hai tam giác vuông MON à APB đồng dạng vị có cắp góc nhọn bằng nhau.
b)
Tam giác AM = MP, BN = NP (1) (tính chất hai tiếp tuyến cắt nhau)
Tam giác vuông MON có OP là đường cao nên:
MN.PN = OP2 (2)
Từ 1 và 2 suy ra AM.BN = OP2 = R2
c) Từ tam giác MON đồng dạng với tam giác APB ta có :
Khi AM = thi do AM.BN = R2 suy ra BN = 2R
Do đó MN = MP + PN = AM + BN = + 2R =
Suy ra MN2 =
Vậy =
d) Nửa hình tròn APB quay quanh bán kính AB = 2R sinh ra một hình cầu có bán kính R.
Vậy V = πR3