Bài 3: Hình cầu. Diện tích mặt cầu và thể tích hình cầu.

1. Hình cầu

Quay nửa đường tròn tâm \(O\), bán kính \(R\) một vòng quanh đường kính \(AB\), ta được một hình cầu.

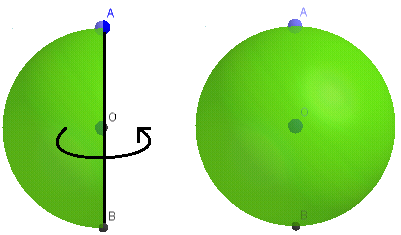
• Nửa đường tròn trong phép quay nói trên tạo thành mặt cầu.
• Điểm \(O\) là tâm, \(R\) là bán kính của hình cầu hay mặt cầu đó.

2. Cắt hình cầu bởi một mặt phẳng

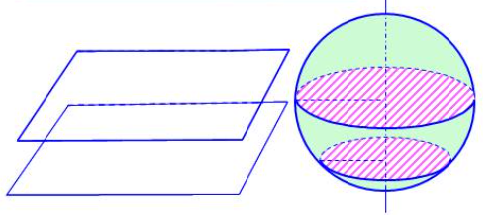
• Khi cắt hình cầu bán kính \(R\) bởi một mặt phẳng, ta luôn được mặt cắt là một hình tròn.
• Khi cắt mặt cầu bán kính \(R\) bởi một mặt phẳng, ta được một đường tròn:

+) Đường tròn này có bán kính \(R\) nếu mặt phẳng đi qua tâm. Khi đó, người ta gọi đường tròn này là đường tròn lớn.

+) Đường tròn có bán kính nhỏ hơn \(R\) nếu mặt phẳng không đi qua tâm.

3. Diện tích mặt cầu

Ở lớp dưới ta đã biết:

Diện tích mặt cầu được tính bởi công thức:

\(S=4\pi R^2\) hay \(S=\pi d^2\)

trong đó \(R,d\) lần lượt là bán kính và đường kính mặt cầu.

Ví dụ 1: Tính diện tích mặt cầu có bán kinh·\(3cm\)?

Ta có: \(S=4\pi3^2=36\pi\left(cm^2\right)\).

Ví dụ 2: Một hình cầu có diện tích \(120\pi\left(cm^2\right)\). Tính bán kính của nó?

Ta có: \(120\pi=4\pi R^2\Rightarrow R^2=30\Rightarrow R=\sqrt{30}\left(cm\right)\).

Ví dụ 3: Cắt mặt cầu bởi một mặt phẳng đi qua tâm, ta được đường tròn có diện tích \(16\pi\). Tính diện tích mặt cầu?

Ta có: \(\pi R^2=16\pi\Rightarrow R^2=16\Rightarrow R=4\).

Do đó, diện tích mặt cầu là: \(S=4\pi R^2=4\pi4^2=64\pi\) (đơn vị diện tích).

4. Thể tích hình cầu

Bằng thực nghiệm, người ta chứng minh được rằng:

Thể tích hình cầu bán kính \(R\) được tính bởi công thức:

\(V=\dfrac{4}{3}\pi R^3\)

Ví dụ 1: Tính thể tích hình cầu có bán kính \(3cm\)?

Ta có: \(V=\dfrac{4}{3}\pi3^3=36\pi\left(cm^3\right)\).

Ví dụ 2: Một hình cầu có diện tích \(16\pi\left(cm^2\right)\). Tính thể tích hình cầu?

Ta có: \(4\pi R^2=16\pi\Rightarrow R^2=4\Rightarrow R=2\left(cm\right)\).

\(\Rightarrow\) Thể tích hình cầu là: \(V=\dfrac{4}{3}\pi R^3=\dfrac{4}{3}\pi.2^3=\dfrac{32}{3}\pi\left(cm^3\right)\).