Cạnh hình vuông là: \(a = \sqrt 5 = 2,236...\)(m)
Ta có: \(2,236... < 2,361\) nên a<b.
Cạnh hình vuông là: \(a = \sqrt 5 = 2,236...\)(m)
Ta có: \(2,236... < 2,361\) nên a<b.
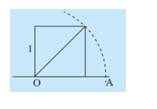
Quan sát hình vẽ bên và cho biết độ dài của đoạn thẳng OA bằng bao nhiêu. Độ dài OA có là số hữu tỉ hay không?
Hãy so sánh các số thập phân sau đây: 3,14; 3,14(15); 3,141515
Không cần vẽ hình, hãy nêu nhận xét về vị trí của hai số \(\sqrt 2 \,;\frac{3}{2}\) trên trục số.
So sánh các số đối của hai số \(\sqrt 2 \) và \(\sqrt 3 \).

Gọi A và A' lần lượt là hai điểm biểu diễn hai số 4,5 và -4,5 trên trục số. So sánh OA và OA'.
So sánh hai số thực:
a) 4,(56) và 4,56279;
b) -3,(65) và -3,6491;
c) 0,(21) và 0,2(12);
d) \(\sqrt 2 \) và 1,42.
Trên 2 trục số, so sánh khoảng cách từ điểm 0 đến hai điểm \(\sqrt 2 \) và \( - \sqrt 2 \).

Các phát biểu sau đúng hay sai? Nếu sai, hãy phát biểu lại cho đúng.
\(a)\,\sqrt 3 \in \mathbb{Q};\,\,\,\,\,\,\,b)\sqrt 3 \in \mathbb{R}\,\,\,\,\,c)\frac{2}{3} \notin \mathbb{R}\,\,\,\,\,d)\, - 9 \in \mathbb{R}\)
Hãy cho biết tính đúng, sai của các khẳng định sau:
a) \(\sqrt 2 ;\,\sqrt 3 ;\,\sqrt 5 \) là các số thực.
b) Số nguyên không là số thực.
c) \( - \frac{1}{2};\frac{2}{3};\, - 0,45\) là các số thực.
d) Số 0 vừa là số hữu tỉ vừa là số vô tỉ.
e) 1; 2; 3; 4 là các số thực.