Bài 4: Khái niệm hai tam giác đồng dạng
Các câu hỏi tương tự
Hình bình hành ABCD có AB=8cm; AD=6cm, M là điểm thuộc BC sao cho BM = 4cm, AM cắt đường chéo BD tại I và cắt DC tại N.
a. Tính tỉ số \(\dfrac{IB}{ID}\)
b. Chứng minh: \(\Delta MAB\sim\Delta AND\)
c. Tính DN, CN.
d. Biết K nằm trên đường thẳng AB và K là trung điểm AB, KM cắt CN tại K'. Chứng minh K' là trung điểm của CN.
Hình bình hành ABCD có AB=8cm; AD=6cm, M là điểm thuộc BC sao cho BM = 4cm, AM cắt đường chéo BD tại I và cắt DC tại N.
a. Tính tỉ số \(\dfrac{IB}{ID}\)
b. Chứng minh: \(\Delta MAB\sim\Delta AND\)
c. Tính DN, CN.
d. Biết K nằm trên đường thẳng AB và K là trung điểm AB, KM cắt CN tại K'. Chứng minh K' là trung điểm của CN
cho hình vuông ABCD có độ dài cạnh bằng 2 cm. Gọi E,F theo thứ tự là trung điểm của AD,DC. Gọi I,H theo thứ tự là giao điểm của AF với BE,BD. Tính S tứ giác EIHD. (làm giúp mik bài này)
cho hình thang abcd (ab//cd) có m là giao điểm của ad và c, n là giao điểm của hai đường chéo .Gọi i và k theo thứ tự là giao điểm cua mn vói ab và cd.Chứng minh rằng :
a)ai/dk=ib/kc,ai/kc=ib/dk
b)i là trung điểm của ab,k là trung điểm của cd
Cho tam giác ABC vuông tại A, ẻ đường cao AH ( H \(\in\)BC), biết AB=9cm, AC=12cm. Gọi M,N lần lượt là trung điểm của AB,AC.
a. CMR: \(\Delta AMN\sim\Delta ABC\)
b. Tính BC, AH?
c. Qua N kẻ NP // AB (P\(\in\)BC). Chứng minh rằng \(\dfrac{S_{NPC}}{S_{ABC}}\)
Hình thang ABCD (AB//CD) có CD = 2AB. Gọi E là trung điểm của DC (h.21).
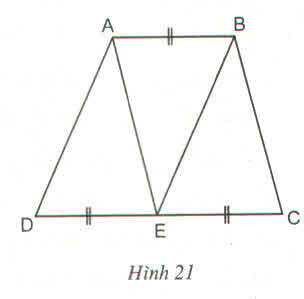
Chứng minh rằng 3 tam giác ADE, ABE và BEC đồng dạng với nhau từng đôi một. (Chú ý viết các đỉnh của hai tam giác đồng dạng theo thứ tự tương ứng với nhau)
Cho Delta DEG nhọn có 3 đường cao DM, EN, GP cắt nhau tại H
a, CM: DP.DEDN.DG; EP.DEEM.EG; GN.DGGM.GE
b, CM: HM.HD HE.HN HP.HG
c, CM: Delta DPNsimDelta DGE; Delta EPNsimDelta EGD; Delta GMNsimDelta GDE
d, CM: Delta DEHsimDelta DGE; Delta DHGsimDelta PHM; Delta EHGsimDelta PHN
e, CM: MH là phân giác góc PMN, NH là phân giác góc PNM, PH là phân giác góc NPM
f, CM H cách đều 3 cạnh Delta MNP
g, CM EH.EN+HG.GPEG^2, DH.DM+GH.GP DG^2, DH.MD+EH.ENED^2
h, Kẻ ExperpED, Gyperp GD. Ex cắt Gy tại K....
Đọc tiếp
Cho \(\Delta DEG\) nhọn có 3 đường cao DM, EN, GP cắt nhau tại H
a, CM: DP.DE=DN.DG; EP.DE=EM.EG; GN.DG=GM.GE
b, CM: HM.HD= HE.HN= HP.HG
c, CM: \(\Delta DPN\sim\Delta DGE\); \(\Delta EPN\sim\Delta EGD\); \(\Delta GMN\sim\Delta GDE\)
d, CM: \(\Delta DEH\sim\Delta DGE\); \(\Delta DHG\sim\Delta PHM\); \(\Delta EHG\sim\Delta PHN\)
e, CM: MH là phân giác góc PMN, NH là phân giác góc PNM, PH là phân giác góc NPM
f, CM H cách đều 3 cạnh \(\Delta MNP\)
g, CM EH.EN+HG.GP=\(EG^2\), DH.DM+GH.GP= \(DG^2\), DH.MD+EH.EN=\(ED^2\)
h, Kẻ Ex\(\perp\)ED, \(Gy\perp GD\). Ex cắt Gy tại K. Gọi I là trung điểm BC. CM BHCM là HBH và H,I,K thẳng hàng
i, Gọi O là trung điểm của DK. CM OI song song DH và OI=\(\frac{1}{2}\)DH
j, CM O là tâm đường tròn ngọi tiếp \(\Delta DEF\)
cho tam giác abc vuông cân tại a đường cao AH ( H thuộc BC ). Goi E là trung điểm của AC, K là chân đừng vuôn góc kẻ từ H xuống AB. Tứ giác AEHK là hình gì ?
cho tam giác ABC nhọn, AB<AC .Trên cạnh AB lấy điểm D(D khác A và B),trên cạnh AC lấy điểm E sao cho góc ADE = ACB
a) CM : tam giác ADE đồng dạng tam giác ACB
b)Gọi i là giao điểm của BC và DE. CM: IB.IC=ID.IE
c)Lấy M là trung điểm BC . CM \(\dfrac{AD.AB}{AE.AM}\) =2









