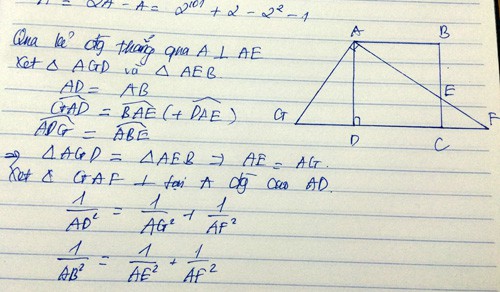Kẻ AG⊥AF
Xét △ABE và △ADG có
\(\widehat{BAE}=\widehat{DAG}\) (cùng phụ góc DAF)
\(\widehat{ABE}=\widehat{ADG}=90^o\)
suy ra △ABE=△ADG
=> AE=AG(2 cạnh tương ứng)
Xét △AGF vuông tại A đường cao AD, Ta có:
\(\dfrac{1}{AD^2}=\dfrac{1}{AG^2}+\dfrac{1}{AF^2}\)
\(\Leftrightarrow\dfrac{1}{AB^2}=\dfrac{1}{AE^2}+\dfrac{1}{AF^2}\)
Cho hình vuông ABCD có cạnh a , Qua đỉnh A vẽ đường thẳng cát BC tại M , cắt CD tại I . CMR :
\(\dfrac{1}{AM^2}+\dfrac{1}{AI^2}=\dfrac{1}{a^2}\)
Giúp mình với
Cho hình chữ nhật ABCD có AB=3AD , điểm E thuộc cạnh BC , AE cắt DC tại F
CMR: \(\dfrac{9}{AB^2}=\dfrac{9}{AE^2}+\dfrac{1}{AF^2}\)
cho hình vuông ABCD , cạnh có độ dài bằng a . E là 1 điểm di động trên CD(E khác C,D).AE cắt BC tại F ,kẻ đường thẳng vuông góc với AE tại A cắt CD tại K
a,Chứng minh:1/AF^2+1/AE^2=không đổi
b,chứng minh : cosAKE=sinEKF.cosEFK+sinEFK.cosEKF
Cho hình vuong ABCD. Lấy điểm E trên BC, tia AE cắt đường thẳng CD tại G. Trên nửa mp bờ là đường thẳng AE chứa tia AD, kẻ AF vuông góc với AE và AF=AE.
a) Chứng minh 3 điểm F,D,C thẳng hàng
b) \(\dfrac{1}{AB^2}=\dfrac{1}{AE^2}+\dfrac{1}{AG^2}\)
Cho hình vuông ABCD cạnh a. Gọi M là một điểm nằm giữa B và C. Tia AM cắt đường thẳng CD tại N. Chứng minh giá trị biểu thức P=\(\dfrac{1}{AM^2}+\dfrac{1}{AN^2}\) luôn không đổi khi M di chuyển trên B và C
Cho hình chữ nhật ABCD có diện tích 2,34567 cm2. Lấy các điểm M, N, P lần lượt thuộc các cạnh AB, BC, CD sao cho \(\dfrac{AM}{MB}=\dfrac{1}{2};\dfrac{BN}{NC}=\dfrac{2}{3};\dfrac{CP}{PD}=\dfrac{3}{4}\). Gọi E là giao điểm của CM và DN. Đường thẳng qua E và song song với AB cắt AP tại F. Đường thẳng BF cắt AD tại Q. Tính diện tích tam giác PEQ.
- Toán 9 CASIO -
Cho nửa đường tròn tâm O đường kính AB. Lấy điểm C thuộc AO ( C # A và B). Đường thảng qua C vuông góc AB cắt (O) tại D. E là trung điểm của CD. Tia AE cắt (O) tại M.
a) Chứng minh BCEM nội tiếp
b) Cm góc AMD + DAM = DEM
c) Tiếp tuyến của (O) tại D cắt đường thẳng AB tại F. Cm FD2 = FA . FB và \(\dfrac{CA}{CD}=\dfrac{FD}{FB}\)
d) Gọ (I;r) là đg tròn ngoại tiếp tam giác DEM. Giả sử r = \(\dfrac{CD}{2}\). Chứng minh CI // AD
Cho hình vuông ABCD có cạnh bằng a.Đường thẳng qua đỉnh C cắt AB và AD kéo dài tại F và E.
a.Chứng minh rằng :DE.BF không đổi
b. Chứng minh :\(\dfrac{DE}{BF}=\dfrac{AE^2}{ÀF^2}\)
Từ điểm A ở ngoài đường trong (O), kẻ hai tiếp tuyến AB,AC tới đường tròn ( B,C là các tiếp điểm ). Đường thẳng qua A cắt đường tròn (O) tại D và E( D nằm giữa A và E, dây DE không qua tâm O ). Gọi H là trung điểm của DE, AE cắt BC tại K.
a) C/m ABOC nt đường tròn .
b) C/m HA là tia phân giác của góc BHC
c ) Chứng minh : \(\dfrac{2}{AK}=\dfrac{1}{AD}+\dfrac{1}{AE}\)
D ) Đường thẳng kẻ qua D vuông góc OB cắt BE tại F, cắt BC ở I. Chứng minh : ID = IF
