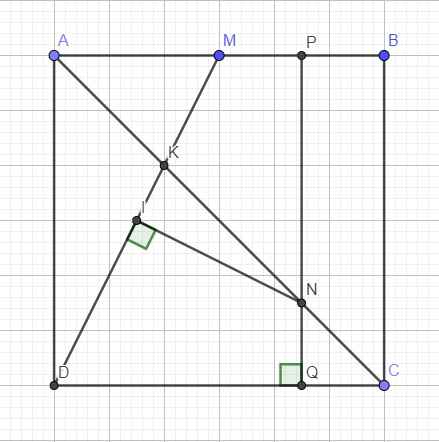
Đặt \(AB=a\), qua N kẻ đường thẳng song song BC cắt AB và CD lần lượt tại P và Q
Theo Talet: \(\Rightarrow\dfrac{NQ}{AD}=\dfrac{CQ}{CD}=\dfrac{CN}{AC}=\dfrac{1}{4}\Rightarrow\left\{{}\begin{matrix}NQ=\dfrac{a}{4}\Rightarrow NP=\dfrac{3a}{4}\\CQ=BP=\dfrac{a}{4}\Rightarrow DQ=AP=\dfrac{3a}{4}\\\end{matrix}\right.\)
Pitago tam giác ADM: \(DM^2=AM^2+AD^2=\dfrac{5a^2}{4}\)
Pitago tam giác MNP: \(MN^2=MP^2+PN^2=\dfrac{5a^2}{8}\)
Pitago tam giác DQN: \(DN^2=DQ^2+QN^2=\dfrac{5a^2}{8}\)
\(\Rightarrow\left\{{}\begin{matrix}MN=DN\\MN^2+DN^2=DM^2\end{matrix}\right.\) \(\Rightarrow\Delta DMN\) vuông cân tại N
Gọi I là trung điểm DM \(\Rightarrow IN\perp DM\)
Phương trình đường thẳng qua N và vuông góc DM có dạng:
\(0\left(x+\dfrac{3}{2}\right)+1\left(y-\dfrac{1}{2}\right)=0\Leftrightarrow y-\dfrac{1}{2}=0\)
Tọa độ I là nghiệm: \(\left\{{}\begin{matrix}x-1=0\\y-\dfrac{1}{2}=0\end{matrix}\right.\) \(\Rightarrow I\left(1;\dfrac{1}{2}\right)\)
\(\Rightarrow\overrightarrow{IN}=\left(-\dfrac{5}{2};0\right)\Rightarrow IN=\dfrac{5}{2}\)
\(\Rightarrow DI=IN=\dfrac{5}{2}\)
Do D thuộc x-1=0 nên tọa độ có dạng \(D\left(1;d\right)\) \(\Rightarrow\overrightarrow{ID}=\left(0;d-\dfrac{1}{2}\right)\)
\(\Rightarrow\left|d-\dfrac{1}{2}\right|=\dfrac{5}{2}\Rightarrow d=-2\)
\(\Rightarrow D\left(1;-2\right)\)
Từ đây dễ dàng xác định tọa độ các điểm còn lại.
Gọi K là giao điểm AC và DM, theo Talet:
\(\dfrac{AK}{CK}=\dfrac{KM}{DK}=\dfrac{AM}{DC}=\dfrac{1}{2}\Rightarrow\left\{{}\begin{matrix}DK=\dfrac{2}{3}DM=\dfrac{4}{3}DI\\AK=\dfrac{1}{3}AC=\dfrac{4}{9}AN\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{DK}=\dfrac{4}{3}\overrightarrow{DI}\Rightarrow\) tọa độ K
\(\overrightarrow{AK}=\dfrac{4}{9}\overrightarrow{AN}\Rightarrow\) tọa độ A
Tọa độ D, tọa độ I \(\Rightarrow\) tọa độ M \(\Rightarrow\) tọa độ B
\(\Rightarrow\) Tọa độ C