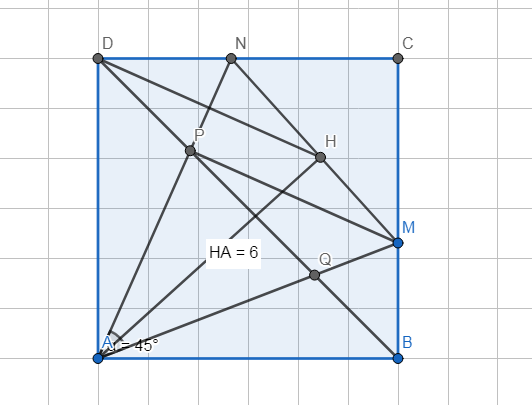
a) △APQ và △BMQ có: \(\widehat{PAQ}=\widehat{MBQ}=45^0;\widehat{AQP}=\widehat{BQM}\).
\(\Rightarrow\)△APQ∼△BMQ (g-g)
\(\Rightarrow\dfrac{QP}{QM}=\dfrac{QA}{QB}\Rightarrow\dfrac{QP}{QA}=\dfrac{QM}{QB}\)
△ABQ và △PMQ có: \(\dfrac{QP}{QA}=\dfrac{QM}{QB};\widehat{AQB}=\widehat{PQM}\)
\(\Rightarrow\)△ABQ∼△PMQ (c-g-c).
b) △ABQ∼△PMQ \(\Rightarrow\dfrac{PM}{AB}=\dfrac{PQ}{AQ};\widehat{BAQ}=\widehat{MPQ}\Rightarrow MP=\dfrac{PQ}{AQ}.AB\)
△APQ và △BPA có: \(\widehat{QAP}=\widehat{ABP}=45^0;\widehat{APB}\) là góc chung.
\(\Rightarrow\)△APQ∼△BPA (g-g)
\(\Rightarrow\widehat{AQP}=\widehat{BAP}\)
\(\widehat{APM}=\widehat{APQ}+\widehat{MPQ}=180^0-45^0-\widehat{AQP}+\widehat{BAQ}=180^0-45^0-\left(\widehat{BAP}-\widehat{BAQ}\right)=180^0-45^0-45^0=90^0\)
\(\Rightarrow\)MP⊥AN tại P.
△MPN và △AHN có: \(\widehat{MPN}=\widehat{AHN}=90^0;\widehat{ANM}\) là góc chung.
\(\Rightarrow\)△MPN∼△AHN (g-g)
\(\Rightarrow\dfrac{AH}{MP}=\dfrac{AN}{MN};\dfrac{NP}{NH}=\dfrac{NM}{NA}\Rightarrow\dfrac{NP}{NM}=\dfrac{NH}{NA}\)
△APQ và △AMN có: \(\dfrac{NP}{NM}=\dfrac{NH}{NA};\widehat{MAN}\) là góc chung.
\(\Rightarrow\)△APQ∼△AMN (c-g-c)
\(\Rightarrow\dfrac{AQ}{AN}=\dfrac{PQ}{MN}\Rightarrow\dfrac{MN}{AN}=\dfrac{PQ}{AQ}\)
\(\dfrac{AH}{MP}=\dfrac{AN}{MN}\Rightarrow AH=MP.\dfrac{AN}{MN}=\dfrac{PQ}{AQ}.AB.\dfrac{AN}{AM}=AB\) không đổi.