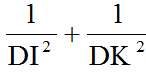Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông
Các câu hỏi tương tự
giúp mk bài này vs Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng:a) Tam giác DIL là một tam giác cânb) Tổngkhông đổi khi I thay đổi trên cạnh AB.
Đọc tiếp
giúp mk bài này vs
Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng:
a) Tam giác DIL là một tam giác cân
b) Tổng
không đổi khi I thay đổi trên cạnh AB.
cho hình vuông ABC , E à điểm năm giữa A và B . Tia DEvà tia CB cắt nhau ở K. kẻ qua D 1 đường thẳng vuống góc với DE cắt đường thẳng BC tại H
CMR: 1) tam giác DEH cân
2) 1 phần DE mũ 2 cộng 1 phần DK mũ 2 không đổi khi E thay đổi trên cạnh AB
cho tam giác ABC vuông tại A có đường cao AH. Gọi E và F lần lượt là hình chiếu của H trên AB,AC. cho BH= 3cm, CH= 12cm
a, tính độ dài các cạnh AB,AC
b, chứng minh HF= 2HE
c, từ C kẻ đường thẳng vuông góc với BC, đường thẳng này cắt đường thẳng AB tại I, kẻ AK vuông góc với CI tại K. chứng minh
CI^3/CB^3= IK/BH
Cho hình vuông ABCD lấy điểm M ∈ BC vẽ AN ⊥ AM; N ∈ CD; tia AM cắt đường thẳng CD tại E.a) ΔANM là tam giác gì?b) Cmr: khi điểm M di động trên cạnh BC thì dfrac{1}{AM^2}+dfrac{1}{AE^2}không đổi A B C D N M
Đọc tiếp
Cho hình vuông ABCD lấy điểm M ∈ BC vẽ AN ⊥ AM; N ∈ CD; tia AM cắt đường thẳng CD tại E.
a) ΔANM là tam giác gì?
b) Cmr: khi điểm M di động trên cạnh BC thì \(\dfrac{1}{AM^2}+\dfrac{1}{AE^2}\)không đổi
Cho đoạn thẳng AB và O là trứng điểm của AB. Trên một nửa mặt phẳng bờ AB kẻ 2 tia Ax, By vuông góc với AB. Một góc vuông đỉnh là O có 2 cạnh cắt Ax, By lần lượt tại C , D. Gọi C là giao điểm của tia CO với tia đối của tia By. Chứng minh:
a, CDC là tam giác cân
b, CD là tiếp tuyến của đường tròn đường kính AB
c, Đường tròn ngoại tiếp tam giác COD luôn tiếp xúc với 1 đường thẳng cố định khi góc vuông tại O thay đổi
Đọc tiếp
Cho đoạn thẳng AB và O là trứng điểm của AB. Trên một nửa mặt phẳng bờ AB kẻ 2 tia Ax, By vuông góc với AB. Một góc vuông đỉnh là O có 2 cạnh cắt Ax, By lần lượt tại C , D. Gọi C' là giao điểm của tia CO với tia đối của tia By. Chứng minh:
a, CDC' là tam giác cân
b, CD là tiếp tuyến của đường tròn đường kính AB
c, Đường tròn ngoại tiếp tam giác COD luôn tiếp xúc với 1 đường thẳng cố định khi góc vuông tại O thay đổi
Cho hình chữ nhật ABCD (AB lớn hơn AC) . Kẻ AH vuông góc BD tại H . AH cắt DC tại K và cắt đường thẳng BC tại M A) Chứng minh DH.DB=AH.AK và BC.BD=AH.AM B) Chứng minh AD bình = DK.DC C) Chứng minh AH bình= HK.HM
Cho tam giác ABC (AB<AC) có góc A bằng 90* và M là trung tuyến của B. Gọi H là hình chiếu của A trên BC. Cho biết AM=13cm; AH=12cm
a) tính MH; AB; AC
b) Đường thẳng qua B và vuông góc với AM cắt AC tại F. Tính AF;BF
Cho tam giác 𝐴𝐵𝐶 có ba góc nhọn, đường cao 𝐵𝐸. Từ E kẻ 𝐸𝐻, 𝐸𝐾 vuông góc với 𝐵𝐴, 𝐵𝐶. a) Chứng minh 𝐵𝐻. 𝐵𝐴 = 𝐵𝐾. 𝐵𝐶 b) Chứng minh ∆𝐵𝐻𝐾~∆𝐵𝐶𝐴. c) Kẻ 𝐶𝐹 vuông góc với 𝐴𝐵, gọi 𝐼 là trung điểm của 𝐸𝐹. Chứng minh ba điểm 𝐻,𝐼,𝐾 thẳng hàng.
cho tam giác ABC vuông tại A, đường cao AH . Cho biết BH =4, CH=9cm. Gọi D,E lần lượt là hình chiếu vuông góc của H trên cạnh AB, AC. Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M,N. Tính diện tích tứ giác DENM
MÌNH ĐANG CẦN GẤP MN GIÚP MIK VS Ạ ! MIK CẢM ƠN !
cho hình chữ nhật ABCD có AB=6cm,AD=32cm.Từ D kẻ đường thẳng vuông góc với đường chéo AC, đường thẳng này cắt AC tại E và cắt AB tại F. Tính EA,EC,ED,FB,FD