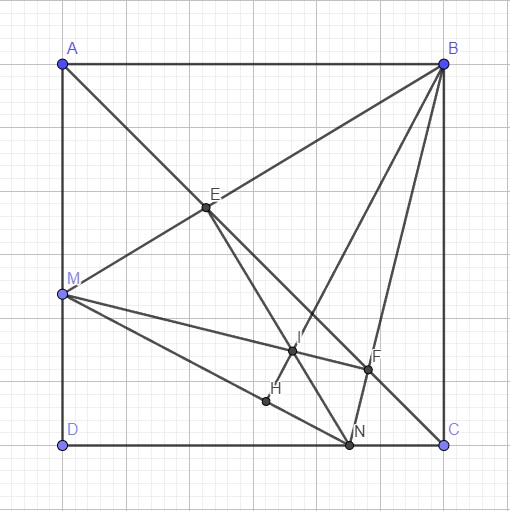
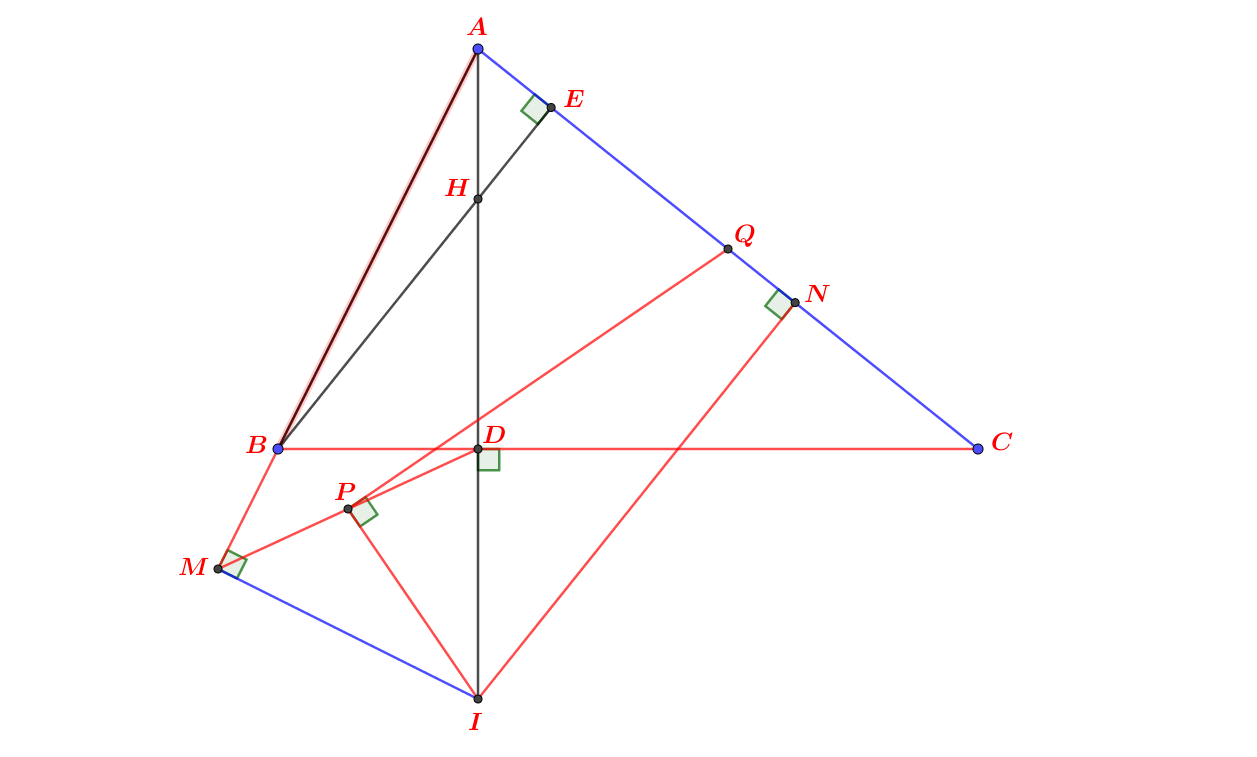
Cho hình vuông ABCD cạnh có độ dài bằng a. Trên cạnh AD lấy điểm M và cạnh CD lấy điểm N sao cho góc MBN = 45°. Gọi E và F lần lượt là giao điểm của BM, BN với AC. a/ Chứng minh: Tứ giác BENC nội tiếp, từ đó suy ra NE vuông góc với BM b/ Gọi I là giao điểm của NE và MF. Chứng minh: BI vuông góc với MN. c/ Tìm vị trí của M và N để diện tích tam giác MDN lớn nhất. Tính diện tích lớn nhất đó theo a.
a.
DO ABCD là hình vuông \(\Rightarrow\widehat{ACD}=45^0\)
\(\Rightarrow\widehat{ACD}=\widehat{EBN}\)
Mà \(\widehat{ACD}\) và \(\widehat{EBN}\) cùng chắn EN
\(\Rightarrow\) Tứ giác BENC nội tiếp
\(\Rightarrow\widehat{BEN}+\widehat{BCN}=180^0\)
\(\Rightarrow\widehat{BEN}=180^0-\widehat{BCN}=180^0-90^0=90^0\)
\(\Rightarrow NE\perp BM\) tại E
b.
Tương tự ta có tứ giác ABFM nội tiếp (\(\widehat{MAF}=\widehat{MBF}=45^0\) cùng chắn MF)
\(\Rightarrow\widehat{BFM}+\widehat{BAM}=180^0\)
\(\Rightarrow\widehat{BFM}=90^0\Rightarrow MF\perp BN\)
\(\Rightarrow I\) là trực tâm của tam giác BMN
\(\Rightarrow BI\perp MN\)
c.
Gọi H là giao điểm BI và MN
Do E và F cùng nhìn MN dưới 1 góc vuông
\(\Rightarrow\) Tứ giác EFMN nội tiếp
\(\Rightarrow\widehat{EMN}+\widehat{EFN}=180^0\)
Mà \(\widehat{EFN}+\widehat{EFB}=180^0\)
\(\Rightarrow\widehat{EMN}=\widehat{EFB}\)
Lại có tứ giác ABFM nội tiếp (A và F cùng nhìn BM dưới 1 góc vuông)
\(\Rightarrow\widehat{EFB}=\widehat{AMB}\) (cùng chắn AB)
\(\Rightarrow\widehat{EMN}=\widehat{AMB}\)
\(\Rightarrow\Delta_VAMB=\Delta_VHMB\left(ch-gn\right)\)
\(\Rightarrow AM=HM\)
Đồng thời suy ra \(AB=BH\Rightarrow BH=BC\) (do AB=BC)
Theo Pitago: \(\left\{{}\begin{matrix}HN=\sqrt{BN^2-BH^2}\\CN=\sqrt{BN^2-BC^2}\end{matrix}\right.\) \(\Rightarrow CN=HN\)
\(\Rightarrow AM+CN=MH+NH=MN\)
\(\Rightarrow MD+DN+MN=MD+DN+AM+CN=AD+CD=2a\)
Pitago: \(MN^2=DM^2+DN^2\ge\dfrac{1}{2}\left(DM+DN\right)^2\Rightarrow MN\ge\dfrac{\sqrt{2}}{2}\left(DM+DN\right)\)
\(\Rightarrow2a-\left(DM+DN\right)\ge\dfrac{\sqrt{2}}{2}\left(DM+DN\right)\)
\(\Rightarrow2a\ge\left(\dfrac{2+\sqrt{2}}{2}\right)\left(DM+DN\right)\ge\left(2+\sqrt{2}\right).\sqrt{DM.DN}\)
\(\Rightarrow DM.DN\le\left(6-4\sqrt{2}\right)a^2\)
\(\Rightarrow S_{MDN}=\dfrac{1}{2}DM.DN\le\left(3-2\sqrt{2}\right)a^2\)
Dấu "=" xảy ra khi \(DM=DN=\left(\sqrt{6}-\sqrt{2}\right)a\)