Bài giải:
Do ABCD là hình thang cân nên AD = BC, AC = BC,
Xét hai tam giác ADC và BCD, ta có: 
AD = BC (gt)
AC = BD (gt)
DC chung
Nên ∆ADC = ∆BCD (c.c.c)
Suy ra
Do đó tam giác ECD cân tại E, nên EC = ED
Ta lại có: AC = BD suy ra EA = EB
Chú ý: Ngoài cách chứng minh ∆ADC = ∆BCD (c.c.c) ta còn có thể chứng minh ∆ADC = ∆BCD (c.g.c) như sau:
AD = BC, , DC là cạnh chung.
Cho hình thang cân ABCD (AB//CD) Elaf giao điểm của 2 đg chéo . CM EA=EB EC= ED
Cho hình thang ABCD ( AB//CD ), E là giao điểm của 2 đường chéo. CM EA = EB, EC = ED.
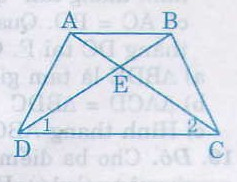
Bài 1: Cho hình thang cân ABCD ( AB // CD) Gọi E là giao điểm của AC và BD. Chứng minh EA = EB.
Bài 2: Cho hình thang cân ABCD (AB//CD) có AB=3,BC=CD=13(cm). Kẻ các đường cao AK và BH.
a) Chứng minh rằng CH=DK.
b) Tính độ dài BH.
Bài 3: Hình thang cân ABCD (AB//CD) có Cˆ=600, DB là tia phân giác của góc D, AB=4cm.
a) Chứng minh rằng BD vuông góc với BC.
b) Tính chu vi hình thang.
Bài 4 : Cho hình thang MNPQ (MN là đáy nhỏ) có 2 đường chéo MP và NQ cắt nhau tại O và NMPˆ=MNQˆA.
a) Chứng minh tam giác OMN và OPQ cân tại O.
b) Chứng minh tứ giác MNPQ là hình thang cân.
c) Qua O vẽ đường thẳng EF//QP (E∈MQ,F∈NP). Chứng minh MNFE, FEQP là những hình thang cân.
Bài 5: Cho hình thang cân ABCD (AB//CD, AB < CD). AD cắt BC tại O.
a) Chứng minh rằng ΔOAB cân.
b) Gọi I, J lần lượt là trung điểm của AB và CD. Chứng minh rằng ba điểm I, J, O thẳng hàng.
c) Qua điểm M thuộc cạnh AC, vẽ đường thẳng song song với CD, cắt BD tại N. Chứng minh rằng MNAB, MNDC là các hình thang cân.
Bài 1: Cho hình thang cân ABCD ( AB // CD) Gọi E là giao điểm của AC và BD. Chứng minh EA = EB.
Bài 2: Cho hình thang cân ABCD (AB//CD) có AB=3,BC=CD=13(cm). Kẻ các đường cao AK và BH.
a) Chứng minh rằng CH=DK.
b) Tính độ dài BH.
cho hình thang cân ABCD có ab//cd gọi o là giao điểm của 2 đường chéo gọi E là giao điểm của 2 đường thẳng chứa 2 cạnh bên . chứng minh rằng chứng minh EO là đường trung trực của AB
cho hình thang cân ABCD có ab//cd gọi o là giao điểm của 2 đường chéo gọi E là giao điểm của 2 đường thẳng chứa 2 cạnh bên . chứng minh rằng chứng minh eo là đường trung trực của AB
Hình thang cân ABCD có AB // CD, O là giao điểm của hai đường chéo. Chứng minh rằng OA = OB, OC = OD ?
Cho hình thang ABCD cân ( AB//CD). Trên AD lấy điểm E sao cho EA=ED. Trên BC lấy điểm F sao cho FB=FC. Chứng minh hình thang ABEF là hình thang cân
: Cho hình thang ABCD cân có AB // CD và AB < CD. Kẻ các đường cao AE, BF.
a. Chứng minh rằng: DE = CF.
b. Gọi I là giao điểm của 2 đường chéo hình thang ABCD. Chứng minh: IA = IB.
c. Tia DA và tia CB cắt nhau tại O. Chứng minh OI vừa là trung trực của AB vừa là trung trực của DC.
