Vì ABCD là hình thang cân
\(\Rightarrow\widehat{A}+\widehat{D}=180^o\)
Nên: \(\widehat{D}=180^o-\widehat{A}=180^o-65^o=115^o\)
Mặt khác ta có ABCD là hình thang cân nên:
\(\widehat{C}=\widehat{D}=115^o\)
Vậy chọn đáp án A
Vì ABCD là hình thang cân
\(\Rightarrow\widehat{A}+\widehat{D}=180^o\)
Nên: \(\widehat{D}=180^o-\widehat{A}=180^o-65^o=115^o\)
Mặt khác ta có ABCD là hình thang cân nên:
\(\widehat{C}=\widehat{D}=115^o\)
Vậy chọn đáp án A
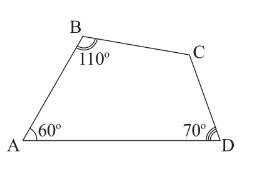
Cho tứ giác \(ABCD\), biết \(\widehat A = 60^\circ ;\;\widehat B = 110^\circ ;\;\widehat D = 70^\circ \). Khi đó số đo góc \(C\) là:
A. \(120^\circ \)
B. \(110^\circ \)
C. \(130^\circ \)
D. \(80^\circ \)
Cho hình hình hành \(ABCD\) có \(AD = 2AB\). Từ \(C\) vẽ \(CE\) vuông góc với \(AB\) tại \(E\). Nối \(E\) với trung điểm \(M\) của \(AD\). Từ \(M\) vẽ \(MF\) vuông góc với \(CE\) tại \(F\), \(MF\) cắt \(BC\) tại \(N\).
a) Tứ giác \(MNCD\) là hình gì?
b) Chứng minh tam giác \(EMC\) cân tại \(M\)
c) Chứng minh rằng \(\widehat {BAD} = 2\widehat {AEM}\)
Hướng dẫn:
a) Chứng minh \(EN = NC = NB = \) \(\frac{1}{2}\) \(BC\)
b) Chứng minh \(\widehat {AEM} = \widehat {EMN} = \widehat {NMC} = \widehat {MCD} = \frac{1}{2}\widehat {NCD}\)
Cho hình thoi \(ABCD\) có cạnh bằng \(13\)cm, độ dài đường chéo \(AC\) là 10cm. Độ dài đường chéo \(BD\) là:
A. 24cm
B. 12cm
C. 16cm
D. 20cm
Cho hình bình hành \(ABCD\) có \(AB = 2AD\). Gọi \(E\) và \(F\) lần lượt là trung điểm của \(DF\) và \(CD\), \(I\) là giao điểm của \(AF\) và \(DE\), \(K\) là giao điểm của \(BF\) và \(CE\)
a) Chứng minh rằng tứ giác \(AECF\) là hình bình hành
b) Tứ giác \(AEFD\) là hình gì? Vì sao?
c) Chứng minh tứ giác \(EIFK\) là hình chữ nhật
d) Tìm điều kiện của hình bình hành \(ABCD\) để tứ giác \(EIFK\) là hình vuông
Cho tam giác \(ABC\) cân tại \(A\). Gọi \(H\), \(D\) lần lượt là trung điểm của các cạnh \(BC\) và \(AB\)
a) Chứng minh rằng tứ giác \(ADHC\) là hình thang
b) Gọi \(E\) là điểm đối xứng với \(H\) qua \(D\). Chứng minh rằng tứ giác \(AHBE\) là hình chữ nhật
c) Tia \(CD\) cắt \(AH\) tại \(M\) và cắt \(BE\) tại \(N\). Chứng minh rằng tứ giác \(AMBN\) là hình bình hành.
Cho hình bình hành \(ABCD\). Các điểm \(E\), \(F\) thuộc đường chép \(AC\) sao cho \(AE = EF = FC\). Gọi \(M\) là trung điểm của \(BF\) và \(CD\), \(N\) là giao điểm của \(DE\) và \(AB\). Chứng minh rằng:
a) \(M\), \(N\) theo thứ tự là trung điểm của \(CD\), \(AB\)
b) \(EMFN\) là hình bình hành
Cho tam giác \(ABC\) vuông tại \(A\) (\(AB < AC\)). Gọi \(M\), \(N\), \(E\) lần lượt là trung điểm của \(AB\), \(AC\), \(BC\)
a) Chứng minh rằng tứ giác \(ANEB\) là hình thang vuông
b) Chứng minh rằng tứ giác \(ANEM\) là hình chữ nhật
c) Qua \(M\) kẻ đường thẳng song song với \(BN\) cắt \(EN\) tại \(F\). Chứng minh rằng tứ giác \(AFCE\) là hình thoi
d) Gọi \(D\) là điểm đối cứng của \(E\) qua \(M\). Chứng minh rằng \(A\) là trung điểm của \(DF\)
Cho tam giác \(ABC\) vuông tại \(A\), đường trung tuyến \(AM\). Biết \(AB = 8\)cm; \(AC = 15\)cm. Độ dài đoạn \(AM\) là:
A. 8,5cm
B. 8cm
C. 7cm
D. 7,5cm
Trong các khẳng định sau, khẳng định nào đúng?
A. Hình chữ nhật có hai đường chép bằng nhau là hình vuông
B. Hình thoi có hai đường chéo vuông góc là hình vuông
C. Hình thoi có một góc vuông là hình vuông
D. Hình chữ nhật có một góc vuông là hình vuông