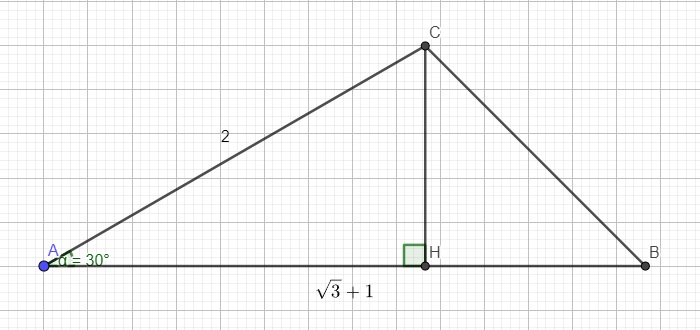
Từ C kẻ CH vuông góc AB
Trong tam giác vuông ACD:
\(CH=AC.sinA=2.sin30^0=1\)
\(AH=AC.cosA=2.cos30^0=\sqrt{3}\)
\(\Rightarrow BH=AB-AH=\sqrt{3}+1-\sqrt{3}=1\)
\(\Rightarrow CH=BH\Rightarrow\Delta BCH\) vuông cân tại H
\(\Rightarrow\widehat{B}=45^0\)
\(a=BC=\sqrt{AH^2+BH^2}=\sqrt{2}\)
\(\widehat{BCH}=45^0\) (do ABH vuông cân)
Trong tam giác vuông ACH:
\(\widehat{ACH}=90^0-\widehat{A}=60^0\)
\(\Rightarrow\widehat{C}=\widehat{ACH}+\widehat{BCH}=105^0\)
Đúng 2
Bình luận (0)
